Необходимое условие оптимальности для задачи оптимального управления системой дифференциальных уравнений в частных производных при наличии фазового ограничения

A NECESSARY CONDITION OF OPTIMALITY FOR A STATE-CONSTRAINED OPTIMAL CONTROL PROBLEM GOUVERNED BY A SYSTEM OF PARTIAL DIFFERENTIAL EQUATIONS

Dmitry Sugak

Candidate of physical and mathematical sciences, assistant Professor, Saint Petersburg State University of Civil Aviation, Russia, Saint Petersburg

Аннотация. В статье рассмотрена задача оптимального управления объектом, описываемым системой дифференциальных уравнений в частных производных. Исследован случай так называемой сингулярной системы уравнений [3]. В такой системе заданному управлению может не соответствовать какое-либо состояние, либо таких состояний может быть бесконечно много. Сформулировано необходимое условие оптимальности в данной задаче - принцип максимума Понтрягина.

Abstract. The article deals with the problem of optimal control of an object described by a system of partial differential equations. The case of the so-called singular system of equations is investigated [3]. In such a system, any state may not correspond to a given control, or there may be an infinite number of such states. A necessary optimality condition in this problem is formulated - the Pontryagin’s maximum principle.

Ключевые слова: дифференциальное уравнение в частных производных; принцип максимума Понтрягина.

Keywords: partial differential equation; Pontryagin’s maximum principle.

1. Введение

В последнее время задачи управления системами дифференциальных уравнений в частных производных стали привлекать всё большее внимание специалистов [6],[7],[8]. Разработке специальных методов, применимых к исследованию задач управления такими системами, посвящены многочисленные работы [3],[4],[5]. Следует, однако, отметить, что в подавляющем большинстве упомянутых работ рассматривалась простейшая постановка задачи. Она характеризуется тем, что множество допустимых процессов, то есть процессов, среди которых ищется минимум некоторого функционала, описывается только дифференциальным уравнением и связанными с ним граничными условиями. В данной работе исследован более общий и сложный случай, когда в описании упомянутого множества присутствуют так называемые фазовые ограничения. Они требуют, чтобы фазовый вектор системы не покидал заданного множества. Это дополнительное требование существенно осложняет исследование задач оптимального управления. В статье на примере задачи оптимального управления эллиптической системой показано как используя принцип максимума Понтрягина [11], [12], [13], [14] подобные трудности можно преодолевать.

2. Задача оптимального управления объектом, описываемым системой уравнений эллиптического типа. Случай фазовых ограничений.

Пусть Ω - открытое и ограниченное подмножество  с липшицевой границей Γ,  - непустое множество и  . Рассмотрим следующую систему уравнений:

                                                                               (2.1)

Здесь  состояние,  управление и  эллиптический дифференциальный оператор второго порядка [1]: , где ,  и  при некотором 

Здесь  - пространство всех непрерывных в  функций, удовлетворяющих условию Гёльдера: . Рассматриваем управления . Решения задачи (2.1) ищем в классе . Напомним, что  – замыкание пространства  - некоторое компактное множество} в . Норма в  определена равенством . Предположим, что заданы функции  и . Рассмотрим задачу оптимального управления:

                                                                                   (2.2)

на множестве

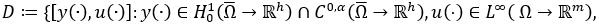
верно (2.1) и 

Считаем, что выполнены следующие предположения:

1. Для почти всех  функция  непрерывна по  вместе с производной . Для всех  функция  измерима по  и для любого  при некотором  справедлива оценка  для почти всех  и всех  c .

2. Для почти всех  функция  непрерывна по  вместе с производной . Для любых  функция  измерима по . Существует такое , что для любого  при некотором  справедлива оценка  для почти всех  и любых  c .

3. Функции  непрерывны по  вместе с производной  и .

Обозначим через  пространство всех вещественных регулярных борелевских зарядов в . Его можно отождествить с двойственным к  пространством [2], где . Символом , обозначим замыкание пространства  в . В  рассматривается норма .

Теорема 2.1.

Пусть выполнены предположения 1-3 и  – оптимальный процесс в задаче (2.2). Тогда существует функция , где , заряды  и число  такие, что

                                                    (2.3)

  для почти всех .                                                              (2.4)

, , .                                                         (2.5)

                                                                                    (2.6)

Здесь  – функция Гамильтона и

 ,

где

,

.

В равенстве (2.3) все слагаемые трактуются как обобщенные функции [9],[10]. Оно представляет собой уравнение эллиптического типа второго порядка относительно . Включение  подразумевает выполнение однородного граничного условия Дирихле . Уравнение вида (2.3) с мерами  было изучено в [2]. В силу (2.1) , откуда согласно предположению 3 . Поэтому в соответствии с включением из (2.5) .