Вычисление интегралов некоторых функций без использования интегрирования по частям
Конференция: VII Международная научно-практическая конференция "Научный форум: технические и физико-математические науки"
Секция: Вещественный, комплексный и функциональный анализ

VII Международная научно-практическая конференция "Научный форум: технические и физико-математические науки"
Вычисление интегралов некоторых функций без использования интегрирования по частям
Calculation of integrals of some functions without partial integration
Alexey Belousov
candidate of engineering sciences, assistant professor in Bryansk State Technical University – BSTU, Russia, Bryansk
Аннотация. В статье рассматривается подход к нахождению неопределённых интегралов для функций множеств, замкнутых относительно дифференцирования, без применения интегрирования по частям. Подход основывается на использовании метода неопределённых коэффициентов. Выполняется сравнение эффективности с традиционно используемым методом интегрирования по частям.
Abstract. The article is devoted to one method for indefinite integrals calculation for functions of sets, closed for differentiation. Our approach doesn’t use partial integration; it is based on the method of undetermined coefficients. We also compare an efficiency of this method and partial integration.
Ключевые слова: неопределённый интеграл; интегрирование по частям; метод неопределённых коэффициентов; замкнутое множество.
Keywords: indefinite integral; partial integrations; method of undetermined coefficients; closed set.
Интегрирование функций является одной из наиболее сложных операций математического анализа, особенно в случаях, когда подынтегральная функция является произведением или композицией нескольких элементарных функций. Для вычисления неопределённого интеграла произведения двух и более элементарных функций, непрерывно дифференцируемых на своей области определения, а также в ряде других случаев, распространённым методом является интегрирование по частям. Данный метод позволяет интегрировать многие функции, тяжело поддающиеся интегрированию другими методами, однако он в общем случае трудоёмок и характеризуется высокой вероятностью ошибок при использовании, причём эти ошибки сложны в обнаружении [5, с. 341]. В некоторых случаях, традиционно предполагающих интегрирование по частям, возможно избежать его. Рассмотрим, каким образом это сделать, пользуясь понятием множеств, замкнутых относительно дифференцирования, и основываясь на сведении задачи интегрирования к задаче дифференцирования. Хотя интегрирование и дифференцирование − взаимообратные, ошибочно полагать, что по уровню сложности это примерно равные задачи. Интегрирование в общем случае − намного более сложная задача, поскольку требует большого опыта и умения заметить, к какому методу интегрирования следует свести исходный интеграл [5, с. 340].
Примеры множеств, замкнутых относительно операций, в учебной литературе обычно сводятся к операциям над числами. Так, ряд подобных примеров представлен в [1, с. 13-14] и [3]. Менее тривиальный пример замкнутого множества − множество элементарных функций вида ![]() , с операцией дифференцирования, поскольку производная элементарной функции тоже элементарная функция [4]. С практической точки зрения, интерес вызывают подмножества элементарных функций, замкнутые относительно дифференцирования и описываемые конечным числом параметров.
, с операцией дифференцирования, поскольку производная элементарной функции тоже элементарная функция [4]. С практической точки зрения, интерес вызывают подмножества элементарных функций, замкнутые относительно дифференцирования и описываемые конечным числом параметров.
Знание о замкнутости относительно дифференцирования даёт важную информацию: первообразная, не считая произвольную постоянную, во многих случаях (хотя и не всегда) будет иметь такой же вид, как и интегрируемая функция, но с другими значениями параметров. Если вид первообразной и интегрируемой функций одинаковый, интегрирование сводится к методу неопределённых коэффициентов. Дифференцируется функция с неопределёнными коэффициентами, путём решения системы линейных алгебраических уравнений (СЛАУ) относительно неопределённых коэффициентов восстанавливаются коэффициенты первообразной.
Так, замкнутым является всякое множество вида ![]() , где Pn − полином степени не выше n, значения a, n фиксированы (обозначим данное множество как EP(a, n)). Это может быть доказано следующим образом. При n>0 верно следующее:
, где Pn − полином степени не выше n, значения a, n фиксированы (обозначим данное множество как EP(a, n)). Это может быть доказано следующим образом. При n>0 верно следующее:
 ,
,
где Qn также полином степени не выше n. При a=0 выполненные преобразования остаются корректными: функция вида ![]() вырождается в константу, но дифференцирование экспоненты по правилу
вырождается в константу, но дифференцирование экспоненты по правилу ![]() даст 0 при a=0, как и дифференцирование константы. При n=0 свойство также выполняется, поскольку константа рассматривается как полином нулевой степени, то есть функции вида
даст 0 при a=0, как и дифференцирование константы. При n=0 свойство также выполняется, поскольку константа рассматривается как полином нулевой степени, то есть функции вида ![]() принадлежат EP(a, 0).
принадлежат EP(a, 0).
EP(a, n) описывается n+2 параметрами: это коэффициент a и n+1 коэффициент полинома. Интегрирование функций на EP(a, n) при n>0 сводится к решению СЛАУ порядка не выше n+1. Неизвестные − коэффициенты при полиноме в первообразной, а значение a в первообразной совпадает с таковым в подынтегральной функции.
Приведём пример. Пусть требуется найти интеграл
![]()
Исходная функция на множестве EP(2, 1). Требуется искать первообразную в виде ![]() . Дифференцируем функцию с неопределёнными коэффициентами p, q:
. Дифференцируем функцию с неопределёнными коэффициентами p, q:
![]()
Восстанавливаем значения коэффициентов:
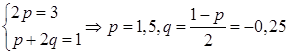
Для сравнения приведём решение с помощью интегрирования по частям:
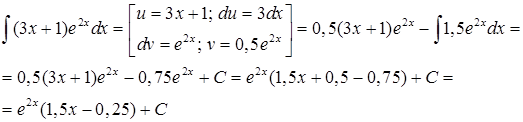
Если не считать текстовых комментариев при сравнении длины математических выкладок и учесть сложность выполняемых операций для человека, интегрирование по частям оказывается нерациональным.
Практически важным является вопрос, какой из методов рациональнее при высоких значениях n. Интегрирование по частям для функции вида ![]() сводится к интегрированию функции того же вида, но со степенью полинома на 1 ниже, делается это за O(n) операций. Всего требуется до n раз воспользоваться формулой интегрирования по частям, следовательно, трудоёмкость составляет O(n2) операций, не считая упрощения полученных выражений путём приведения подобных слагаемых.
сводится к интегрированию функции того же вида, но со степенью полинома на 1 ниже, делается это за O(n) операций. Всего требуется до n раз воспользоваться формулой интегрирования по частям, следовательно, трудоёмкость составляет O(n2) операций, не считая упрощения полученных выражений путём приведения подобных слагаемых.
Теперь оценим трудоёмкость метода определённых коэффициентов. Первообразная имеет вид ![]() . Её производная:
. Её производная:
![]()
Таким образом, получаем СЛАУ вида:

Матрица СЛАУ является двухдиагональной, СЛАУ может быть решена за O(n) операций. Количество операций, требуемых для составления СЛАУ, также O(n). Таким образом, для полиномов высоких степеней метод неопределённых коэффициентов выигрывает по порядку числа операций. Это важно как при решении человеком, так и в случае программной реализации. Наконец, если при программном решении некоторой задачи требуется вычислять неопределённые интегралы только для функций EP(a, n), то также важно учесть, что алгоритм применения интегрирования по частям окажется относительно трудным для программирования.
Рассмотрим другой пример замкнутого множества, когда интегрирование по частям нерационально. Это множество вида ![]() . В вузовской литературе обычно рассматриваются ситуации p=0 или q=0. Интегрирование по частям применяется дважды, чтобы свести исходный интеграл к нему же самому и решить уравнение относительно интеграла [2, с. 22-23]. Метод неопределённых коэффициентов даст более короткое решение: первообразная функции
. В вузовской литературе обычно рассматриваются ситуации p=0 или q=0. Интегрирование по частям применяется дважды, чтобы свести исходный интеграл к нему же самому и решить уравнение относительно интеграла [2, с. 22-23]. Метод неопределённых коэффициентов даст более короткое решение: первообразная функции ![]() будет иметь тот же вид (не считая произвольную постоянную), но с другими p, q. Требуется свести расчёт двух неизвестных коэффициентов к СЛАУ второго порядка и решить данную СЛАУ, что проще, чем интегрировать по частям. Сравним два метода для интеграла
будет иметь тот же вид (не считая произвольную постоянную), но с другими p, q. Требуется свести расчёт двух неизвестных коэффициентов к СЛАУ второго порядка и решить данную СЛАУ, что проще, чем интегрировать по частям. Сравним два метода для интеграла
![]()
Метод неопределённых коэффициентов:
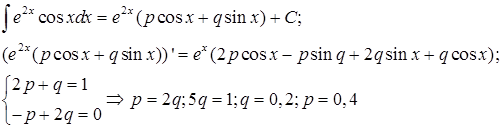
Интегрирование по частям:
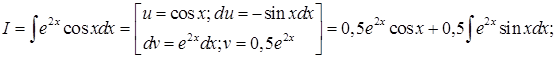
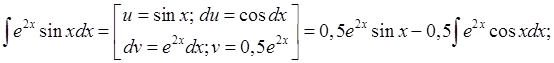

Наиболее очевидный способ получения других замкнутых множеств, для которых можно аналогичным образом применять метод неопределённых коэффициентов, − поиск их среди множеств функций, составленных из двух и более функций следующих классов:
К1) ![]() (экспоненты и константы, a фиксируется);
(экспоненты и константы, a фиксируется);
К2) ![]() (полиномы степени не выше n и константы, n фиксируется; если рассматривать полиномы степени ровно n, то замкнутости нет, например, производная кубической функции не является кубической функций, но всё ещё остаётся функцией вида «полином степени не выше 3»);
(полиномы степени не выше n и константы, n фиксируется; если рассматривать полиномы степени ровно n, то замкнутости нет, например, производная кубической функции не является кубической функций, но всё ещё остаётся функцией вида «полином степени не выше 3»);
К3) ![]() (b фиксируется), может быть также взят более широкий класс функций
(b фиксируется), может быть также взят более широкий класс функций
![]() ,
,
b, q фиксируются.
Например, замкнутым относительно дифференцирования является множество вида ![]() . Следует обратить внимание, что могут быть получены множества, замкнутые относительно операции дифференцирования, но для функций которых при интегрировании первообразная будет не всегда иметь тот же вид, что и интегрируемая функция. Пример − функции, получаемые делением двух полиномов (т.е. функций класса К2): интеграл функции такого вида необязательно того же вида, хотя имеет место замкнутость относительно дифференцирования: производная дроби с полиномами в числителе и знаменателе также дробь с полиномами в числителе и знаменателе. Например, следующая первообразная не сводится к делению полиномов:
. Следует обратить внимание, что могут быть получены множества, замкнутые относительно операции дифференцирования, но для функций которых при интегрировании первообразная будет не всегда иметь тот же вид, что и интегрируемая функция. Пример − функции, получаемые делением двух полиномов (т.е. функций класса К2): интеграл функции такого вида необязательно того же вида, хотя имеет место замкнутость относительно дифференцирования: производная дроби с полиномами в числителе и знаменателе также дробь с полиномами в числителе и знаменателе. Например, следующая первообразная не сводится к делению полиномов:
![]()
Таким образом, замкнутость множества относительно дифференцирования не гарантирует, что при интегрировании функции из данного множества будет получена первообразная на этом же множестве. Однако проще сначала проверить, замкнуто ли множество функций относительно дифференцирования, нежели сразу пытаться определить, как выглядят первообразные для функций множества. Проверка замкнутости относительно дифференцирования – относительно быстрый способ выявления множеств функций, которые целесообразно исследовать на возможность интегрирования функций методом неопределённых коэффициентов.
Подробно опишем один из способов составления замкнутых относительно дифференцирования множеств функций на основе функций, принадлежащих других замкнутым множествам. Пусть S1, S2 − множества, замкнутые относительно дифференцирования (возможно, пересекающиеся). Рассмотрим множество
![]() .
.
Произведение функций f, g имеет вид
![]()
Оба слагаемых принадлежат множеству K4 за счёт замкнутости множеств S1, S2 относительно дифференцирования. Следовательно, если K4 также замкнут относительно сложения, то он замкнут относительно дифференцирования.
Обратим внимание, что оба множества, для которых выше рассмотрены примеры интегрирования, получены именно таким способом. В частности, сложение функций вида ![]() ведёт к сумме вида
ведёт к сумме вида ![]() , будут отличаться только коэффициенты полинома. Поскольку используются полиномы степени не выше n, а не степени ровно n, утверждение верно и в случае, если у слагаемых произведений будут полиномы разных степеней. Аналогично суммирование произведений функций видов K1 и K3 даст сумму того же вида, если оба слагаемых совпадают выражениями в показателе экспоненты и в аргументах тригонометрических функций.
, будут отличаться только коэффициенты полинома. Поскольку используются полиномы степени не выше n, а не степени ровно n, утверждение верно и в случае, если у слагаемых произведений будут полиномы разных степеней. Аналогично суммирование произведений функций видов K1 и K3 даст сумму того же вида, если оба слагаемых совпадают выражениями в показателе экспоненты и в аргументах тригонометрических функций.
Множество произведений функций видов K2 и K3 при одинаковых аргументах тригонометрической функции и значениях n не замкнуто относительно суммирования. Так, функции ![]() являются произведениями данного вида (используются полиномы степени 2), но функция
являются произведениями данного вида (используются полиномы степени 2), но функция ![]() не имеет вид
не имеет вид ![]() .
.
Следует обратить внимание, что при интегрировании с помощью рассмотренного подхода важен правильный выбор замкнутого множества для заданной функции. Пример, не предполагающий использования метода неопределённых коэффициентов, но демонстрирующий суть проблемы, заключается в следующем. Если бы данный подход применялся для интегрирования квадратичной функции, то её нужно было бы рассматривать как полином степени не выше 3, но не как полином степени не выше 2.
Приведём пример использования метода для случая, не сводящегося к К1-К3. Дифференцирование функции вида ![]() приводит к функции схожего вида, но с понижением n на 1:
приводит к функции схожего вида, но с понижением n на 1:
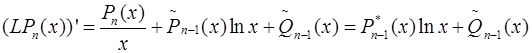 .
.
Исключение из правила − при вырождении полинома P в константу, то есть множество «почти замкнуто» относительно дифференцирования. Если брать обратную операцию, то получим, что всегда интеграл ![]() следует искать на классе
следует искать на классе ![]() .
.
Возможно использование замкнутости относительно дифференцирования и в случае множеств функций более сложной структуры, тяжело поддающихся интегрированию по частям и другим классическим стратегиям интегрирования. Например, интегралы функций ![]() ищутся на множестве
ищутся на множестве
![]() ,
,
где в качестве неопределённых выступают коэффициенты полиномов. Это связано с тем, что множества функций видов ![]() и
и ![]() замкнуты относительно дифференцирования, а суммирование произведений вида
замкнуты относительно дифференцирования, а суммирование произведений вида ![]() при одинаковых b, r даёт множество класса K4.
при одинаковых b, r даёт множество класса K4.
Подводя итог, укажем преимущества и недостатки рассмотренного подхода к интегрированию функций. Основные преимущества заключаются в том, что в ряде случаев интегрирование таким способом намного проще, чем интегрирование по частям, а также характеризуется невысокой вычислительной сложностью, последнее важно в случае программной реализации. Данный подход позволяет легко реализовать взятие неопределённого интеграла в компьютерных программах, когда нужны интегралы функций специальных видов. Основной недостаток − необходимость значительного опыта: человеку, привыкшему использовать традиционные методы интегрирования, сначала будет сложно использовать предложенный. Наконец, класс функций, которые легко интегрируются предложенным способом, ограничен. Частично это компенсируется тем, что для большинства функций легко определить по их виду, будет ли их первообразная по своей структуре им подобна.
Список литературы:
1. Васильев А.В., Мазуров В.Д. Высшая алгебра: В 2 ч.: Конспект лекций. Новосибирск: Новосиб. гос. ун-т., 2010. – 143 c.
2. Ельцов А.А., Ельцова Т.А. Высшая математика. Интегральное исчисление. Дифференциальные уравнения. Томск: Томск. гос. ун-т систем управления и радиоэлектроники, 2003. – 233 с.
3. Что такое замкнутое множество [Электронный ресурс]. – URL: http://scienceland.info/algebra8/closed-set (дата обращения: 5.08.2017)
4. Элементы обшей алгебры [Электронный ресурс]. – URL: http://infopedia.su/5x8fb.html (дата обращения: 5.08.2017)
5. Яриков В.В. Иллюстрирующая программа по нахождению первообразной функции для интеграла вида произведения двух непрерывных гладких функций // Международный журнал «Образовательные технологии и общество». – 2011. – Т. 14, № 1. – С. 337–346.


