Геометрия в Италии в первой половине XX века

Geometry in Italy in the first half of the 20th century

Anastasiia Dulina

PhD student, University “La Sapienza”, Italy, Rome

Аннотация. статья посвящена развитию итальянских школ проективно-дифференциальной геометрии Г. Фубини, К. Сегре, А. Террачини. Рассматриваются теория дифференциальных форм и первая теорема жесткости Г. Фубини, вопросы касательных К. Сегре, классификации многообразий с секущим и тангенциальным дефектом А. Террачини, а также их эволюция и влияние на развитие актуальных проблем проективно-дифференциальной геометрии.

Abstract. The article is devoted to the development of the italian schools of the projective differential geometry of G. Fubini, C. Segre, A. Terracini. The theory of differential forms and the first rigidity theorem of G. Fubini, the questions of С. Segre’s tangents, the classification of secant–defective and tangent-defective varieties of A. Terracini, as well as their evolution and influence on the development of actual problems of the projective differential geometry are considered.

Ключевые слова: проективно-дифференциальная геометрия; дифференциальные формы; теорема жесткости; линейный проективный элемент; уравнения Лапласа; проективно-дифференциальный инвариант.

Keywords: projective differential geometry; differential forms; rigidity theorem; linear projective element; Laplace equations; projective differential invariant.

Одним из выдающихся математиков XX века является итальянский геометр Г. Фубини (G. Fubini, 1879-1943). Первая работа Фубини посвященная проективно-дифференциальной геометрии опубликована в 1914 г., однако его наиболее выдающиеся исследования принадлежат к послевоенному периоду вплоть до 1942 г. Эти исследования были опубликованы в двух трактатах: «Geometria proiettiva differenziale» [3] в 1927 г. и «Introduction à la géométrie projective différentielle des surfaces» [2] в 1931 г., оба написаны в сотрудничестве с Э. Чехом (E. Cech, 1893-1960). Г. Фубини был прежде всего выдающимся специалистом в анализе, что позволило ему преодолеть большие алгоритмические трудности, которые препятствовали открытию «проективно-дифференциальных инвариантов». Фубини предпринял попытку определить поверхность в ординарном пространстве, вплоть до ординарных преобразований в смысле дифференциальных форм. Геометрической интерпретации инвариантов им найденных впоследствии посвятили свои труды разные математики, в частности два выдающихся итальянских геометра А. Террачини и Э. Бомпиани.

В виду этого уместно напомнить, что поверхность в евклидовом трёхмерном пространстве однозначно определена двумя фундаментальными формами, коэффициенты которых проверяют условия совместимости, выраженные уравнениями Кодацци-Маинарди и Гаусса. К 1916 г. Фубини разработал метод для достижения своей цели. Начальная точка Фубини – это концепция касательных К. Сегре и Ж. Дарбу. К. Сегре, который был коллегой Фубини в Туринском университете, задал ему вопрос, является ли достаточным распределение этих касательных для того чтобы охарактеризовать поверхность вплоть до проективных преобразований. Фубини ответил отрицательно на этот вопрос в своей первой заметке, опубликованной в «Annali di Matematica» в 1916 г., но, в то же время, он установил основы своей теории дифференциальных форм и создал инструменты для доказательства его знаменитой теоремы о жесткости.

Согласно Г. Фубини неразложимая поверхность  в  параметрически представлена посредством

Фубини определяет две гомогенных дифференциальных формы [3, с.157]  и .  квадратичная и обращается в нуль вдоль асимптотических направлений, что является аналогом второй метрической фундаментальной формы. кубическая и обращается в нуль вдоль касательных направлений Дарбу.  образуется из кубической части локального выражения  путём наложения на  условия полярности по отношению к , т.е. гессианом  является .  и определяются только до множителя, поэтому только их отношение 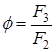 хорошо определено: это называется линейным проективным элементом.

Первая теорема жесткости Фубини: две поверхности имеют один и тот же линейный проективный элемент тогда и только тогда, когда они проективны. Две поверхности  и  проективно применимы, если существует голоморфное, локально обратимое отображение  такое, что, взяв соответствующие точки , , любая кривая с изгибом в  преобразуется в кривую с изгибом в . Первая теорема о жесткости отвечает отрицательно на результаты К. Сегре относительно того, определяет ли распределение касательных линий Дарбу поверхность вплоть до проективного преобразования. Однако это показывает, что данный вопрос имеет смысл: в самом деле,  характеризует квадрики и является расширением дифференциального уравнения коники Монжа.

Параллельно со школой Г. Фубини в Италии развивалась другая геометрическая школа, берущая свои истоки от работ К. Сегре (C. Segre, 1863-1924). Сегре является основателем исследований в области проективно-дифференциальной геометрии гиперпространств с геометрической точки зрения. Он использовал аналитическо-синтетический подход для развития этих теорий. Проективно-дифференциальная геометрия родов высшего порядка была культивируема внутри итальянской школы до 1960-х гг. и разработала ряд фундаментальных результатов, принадлежащих, в частности, итальянскому математику Э. Бомпиани (E. Bompiani, 1889-1975) и его школе. В своих основополагающих работах К. Сегре строго демонстрирует все свойства: геометрические, используя самые простые аналитические инструменты обусловленные глубокой геометрической интуицией. Работа К. Сегре «Su una classe di supeficie degl'iperspazi legata colle equazioni lineari alle derivate parziali di  ordine» [6] опубликованная в 1907 г. является одним из краеугольных камней итальянской школы проективно-дифференциальной геометрии. В этой работе представлены следующие фундаментальные вопросы: поверхность определяет два независимых уравнения Лапласа, если и только если она является разложимой или находится в трёхмерном пространстве; каждая поверхность в  определяет одно уравнение Лапласа; исследование геометрии богатой поверхностями , которые определяют одно уравнение Лапласа в  в связи с поведением их четырёхмерных тангенциальных многообразий; одна поверхность  имеет двойную систему сопряжённых линий, если и только если первая определяет одно уравнение Лапласа. Важные обобщения этих результатов на многомерные многообразия и линейные дифференциальные уравнения высшего порядка были проделаны учениками и последователями К. Сегре, такими как А. Террачини, Э. Бомпиани, Б. Сегре (B. Segre, 1903-1977) и др. Несмотря на то, что точка зрения Г. Фубини отличалась от точки зрения К. Сегре, они имели и точки соприкосновения. В работе «Preliminari di una teoria delle varietà luoghi di spazi» [4, с.110] Сегре изучает многообразия порождённые семейством линейных подпространств. Он связывает тангенциальные свойства этих многообразий с фокальными свойствами генерирующего пространства, широко распространяя концепцию разложимой поверхности. В частности, он основополагает классификацию тангенциально-дефектных многообразий, т.е. многообразий размерности , чьё тангенциальное многообразие имеет размерность меньше ожидаемой, которая равна .

Эта область исследований была продолжена А. Террачини и по-прежнему является открытым полем для исследований. В частности, с тех пор широко используются фокальные свойства, которые в последнее время возрождаются разными авторами с целью выхода на интересные геометрические задачи разного типа.

В работе «Su alcuni punti singolari delle curve algebriche, e sulla linea parabolica di una superficie» [5, с.169-170] К. Сегре представил так называемый контактный инвариант Wolfing–Mehmke–Segre для двух плоских кривых в точке их соприкосновения.

Рассмотрим две кривые  и  имеющие некую точку касания , и их общую касательную . Возьмём общую прямую , проходящую вблизи , которая разрезает ,  и  в точках , , . Зафиксируем общую точку  на . Предел двойного отношения  когда  стремится к прямой через , не зависит от произвольного выбора и является инвариантом, о котором идёт речь.

Принимая более общую точку зрения Э. Вильчинского (E. Wilczynski, 1876-1932) К. Сегре изучает все поверхности  в , параметрически представленные посредством

,

и проверяющие дифференциальное уравнение второго порядка или уравнение Лапласа . Это означает, что первое оскулирующее пространство к  в её общей точке имеет размерность меньшую, чем ожидаемая, и равную 5.

Учитывая поверхность  в  и гладкую точку  на ней, Сегре вводит три касательные линии к  в точке, позже называемые «касательными Сегре», которые расширяют понятие асимптотики линий. Сегре сравнивает эту тройку касательных с другой введённой в 1880 г. тройкой Дарбу, так называемые «касательные Дарбу». Сегре доказывает, что касательные Дарбу сопряжены с его касательными относительно пары асимптотических направлений [5, с.172], исходящих из точки , что немало способствовало развитию школы Г. Фубини.

Эта область исследования была продолжена А. Террачини и Э. Бомпиани и до сегодняшнего дня имеет нерешённые проблемы.

Одним из выдающихся представителей итальянской школы проективно-дифференциальной геометрии является А. Террачини (A. Terracini, 1889-1968). Его труды посвящены классификации многообразий с секущим дефектом и с тангенциальным дефектом: с 1979 г. эта проблема актуализируется в работах Ф. Зака (F. Zak). Сочинения А. Террачини также посвящены геометрически-проективным аспектам теории дифференциальных уравнений в частных производных и классификации многообразий, которые являются решениями многих уравнений Лапласа. Он дал геометрическую интерпретацию теории Г. Фубини, в частности, проективной прямой Фубини-Грина на поверхности и проективной метрики Фубини. Террачини рассмотрел расширения на многомерные проективные многообразия понятия «дифференциальной формы Фубини», заменив его удобными линейными системами. Он классифицировал некоторые особые многообразия, в частности многообразие К. Сегре, отталкиваясь от условий их первой дифференциальной квадратичной формы.

В курсе лекций «Geometria differenziale con particolare riguardo all'indirizzo proiettivo» [7], который А. Террачини читал в 1936-1937 гг. в Туринском университете он представил изучение дифференциальной геометрии в сочетании с разными группами преобразований, в частности, с группой проективных преобразований и, развивая таким образом, дифференциально-проективную геометрию.