Моделирование массопереноса потоком подземных вод в неоднородных средах

Использование моделей подземных вод широко распространено в области наук об окружающей среде [1-5]. Эти модели используются для изучения широкого спектра гидрогеологических условий. Например, определение баланса воды, получение информации о количественных количествах ненасыщенных зон, моделирование потока воды в насыщенных средах, моделирование распространения химических веществ, влияние изменения режима подземных вод на окружающую среду, создание, оптимизация, контроль и создание зон охраны подземных вод. Кроме того, эти модели используются для прогнозирования переноса загрязняющего вещества с целью оценки опасности. Особенность работы заключается в том, что среда является неоднородной, что существенно затрудняет формулировку проблемы и методы ее количественного решения.

Цель работы-разработка алгоритмов для количественного внедрения модели распределения загрязнителей в неравномерной пористой среде подземных вод.

Актуальность работы заключается в определении баланса воды, получении информации о количественных количествах ненасыщенных зон, моделировании потока воды в насыщенных средах,моделировании распространения химических веществ, влиянии изменения режима подземных вод на окружающую среду, создании, оптимизации, контроле и создании зон охраны подземных вод.

В этой работе представлены три разностные схемы, реализующие модель: схема дробления по переменным пространства, параметрическая схема, схема стабилизирующей коррекции. По разносторонней схеме проведено два эксперимента. В ходе проведения данной практики были получены графики.

Постановка задачи. Для описания движения подземных вод используется уравнение Буссинеска следующего типа:

здесь:

x,y – декартные координаты вдоль поверхности Земли;

h – пьезометрическая высота;

, - гидравлическая проводимость по направлениям x и y;

 – объемный поток в одной единице объема, который является условиями глаз и поглощения;

 – коэффициент относительного сохранения, который определяет объем воды, удаляемой из водоема, при изменении высоты на единицу измерения.

, для проводимости известны следующие эмпирические зависимости:

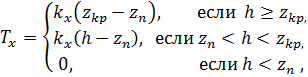
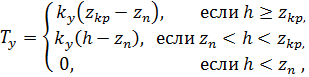
здесь:

, – ,

 – высота основания слоя,

 – высота потолка этажа.

 для функции расчета используется следующая формула расчета:

здесь:

 – коэффициент затяжной вместимости слоя, 

 – коэффициент гравитационной водостойкости.

Транспортировка растворенных веществ в насыщенной среде характеризуется уравнением адвекции-дисперсии следующего вида:

здесь:

 – концентрация растворенного вещества,

 – источники,

, – тензор коэффициента дисперсии,

, – скорость. При этом предполагается, что пористость среды распределена равномерно.

(1), (2) дополняем систему уравнений следующими начальными и пограничными условиями:

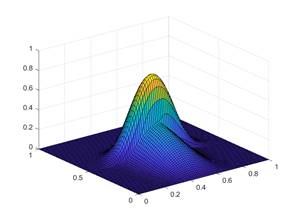
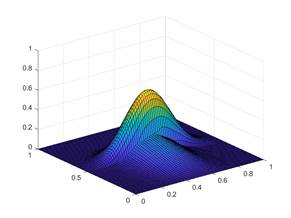
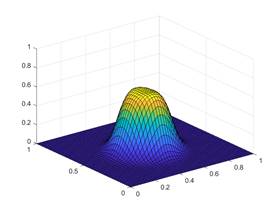
Для реализации модельного числа была разработана программа в среде MatLab, а также проведены числовые вычислительные эксперименты. Результаты вычислительных экспериментов представлены на рисунках 1 и 2

В первой практике в качестве проводящих функций принята простая часть-постоянная функция. По результатам практики средняя разделена на две части,распределение функции h(x, y) в каждой части происходило разным.

Рисунок 1. Результаты первой вычислительной практики

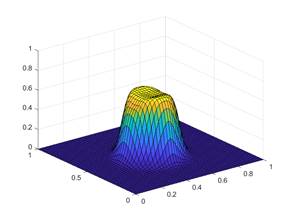
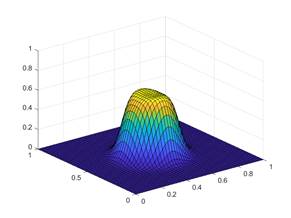
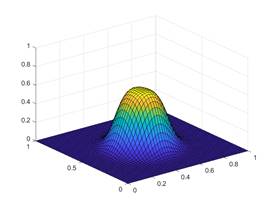
Во второй практике в качестве проводниковых функций приняты более сложные зависимости.

Рисунок 2. Результаты второй вычислительной практики

Таким образом, в этой работе была изучена модель распределения загрязнителя в неравномерной пористой среде подземных вод, сформирован алгоритм ее количественной реализации. С целью изучения устойчивости схем, удалось убедиться в накоплении итерационного процесса, изменяя шаг сетки в широком диапазоне.