ФУНКЦИЯ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА

FUNCTION OF A SINGLE RANDOM ARGUMENT

Djamilya Evloeva

Undergraduate student, Ingush State University, Russia, Magas

Fatima Tsurova

Supervisor, Associate Professor of the Department of Mathematical Analysis, Ingush State University, Russia, Magas

Аннотация. В статье рассматриваются решения различных задач, связанных со случайными явлениями, современная теория вероятностей. Рассмотрены задачи об определении числовых характеристик функции при заданном законе распределения аргументов.

Abstract. The article discusses solutions to various problems related to random phenomena, modern probability theory. The problems of determining the numerical characteristics of a function with a given law of argument distribution are considered.

Ключевые слова: теория вероятностей, закон распределения функции, системы случайных величин, математическое ожидание, дисперсия, закон распределения случайной величины, дискретная случайная величина, плотность случайной величины.

Keywords: probability theory, distribution law of a function, systems of random variables, mathematical expectation, variance, distribution law of a random variable, discrete random variable, density of a random variable.

Если каждому возможному значению случайной величины X соответствует одно возможное значение случайной величины Y, то Y называют Функцией случайного аргумента X:

Y = φ (X).

Пусть задана функция Y = (X) случайного аргумента X, где аргумент X – дискретная случайная величина с возможными значениями X1, X2,… Xn ,вероятности которых соответственно равны P1, P2,… Pn. Очевидно, Y - также дискретная случайная величина с возможными значениями 

Если различным возможным значениям аргумента X соответствуют различные возможные значения функции Y, то вероятности соответствующих значений X и Y между собой равны, так как событие “величина X приняла значение xi” влечет за собой событие “величина Y приняла значение  (xi)”, то вероятности возможных значений Y соответственно равны P1, P2,… Pn.

Пример 1. Дискретная случайная величина X задана распределением

Найти распределение функции Y = X2.

Решение: Имеем, что , следовательно, . Случайная величина X принимает всего два значения: X1 = 2 и X2 = 3 .

Найдем возможные значения Y: Y1 = X12 = 22 = 4; Y2 = X22 = 32 = 9. В данном примере различным возможным значениям аргумента X соответствуют различные возможные значения функции Y, поэтому вероятности соответствующих значений X и Y между собой равны.

Искомое распределение Y:

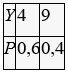
Если различным возможным значениям X соответствуют значения Y, среди которых есть равные между собой, то следует склады

Пример 2. Случайная величина X задана плотностью распределения вероятностей  . Найти дифференциальную функцию случайной величины  .

Решение: Поскольку функциональная зависимость   монотонна на всей числовой

оси, пользуемся готовой формулой  , где   - обратная функция для функции  ; Þ  ;

 ,  ,

Пример 3. Плотность распределения случайной величины Х задана

выражением: 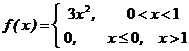 . Определить математическое ожидание и дисперсию случайной величины  .

Решение: Воспользуемся формулами для вычисления математического ожидания и дисперсии функции непрерывного случайного аргумента Х, не находя предварительно закона распределения случайной величины У:

  ;

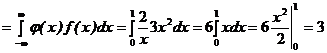Числовые характеристики функции случайного аргумента

Пусть Y = ϕ(х), где X – случайная величина с известным законом распределения, и необходимо определить числовые характеристики Y. 

Однако, если закон распределения величины Y в явном виде не нужен, а необходимы только ее числовые характеристики, применимы следующие формулы.

Если Х – дискретная случайная величина с известным рядом распределения вероятностей, то

Список литературы: