Линейно-конгруэнтный метод и распределение псевдослучайных чисел

Оценивается несовпадение последовательностей псевдослучайных чисел, сгенерированных линейным конгруэнтным методом, что улучшает результат Ягермана. Упоминаются приложения к численному интегрированию.

Пусть m - модуль с примитивным корнем λ, и пусть y₀ - целое число в системе наименьших вычетов по модулю m с НОД (y₀, m) = 1. Мы генерируем последовательность y₀, y₁, ... целых чисел в системе наименьших вычетов по модулю m следующим образом: y_i+1 = λy_i (mod m) для j ≧ 0. Последовательность x₀, x₁, … определяемая как x_i = y_i / m для j ≧ 0, тогда является часто используемой последовательностью псевдослучайных чисел в единичный интервал [0, 1]. Его элементы x_i также могут быть явно описаны как x_i = {λⁱy₀/m}для j ≧ 0, где {x} обозначает дробную часть действительного числа x. Последовательность x₀, x₁, ... имеет период Q = Φ(m), где Φ - функция Эйлера.

Для действительного числа α с 0 ≦ α ≦ 1 пусть A(α) будет количеством элементов последовательности x₀, x₁, ... , x_Q-1, лежащих в интервале [0,α]. Определим невязку D = sup_{0 ≦ α ≦ 1} |A(α) / Q - α|, которая измеряет отклонение от равномерного распределения. Ягерман [2] показал, что D ≦ (4/π) ((3logm) / Q^1/2. Его метод основан на оценке расхождения в терминах определенных тригонометрических сумм. В настоящей заметке мы покажем, что гораздо более простой метод дает значительно более точную оценку для D (см. Теорему 2). Мы доказываем также некоторые связанные результаты.

Для α сверху и положительного целого k пусть A^(k) (α) - количество рациональных чисел i / k, 1 ≦ i ≦ k, НОД (i,k) = 1, лежащих в интервале [0,α].

Теорема 1. Для любого натурального числа k имеем

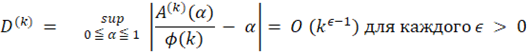
Доказательство. Для произвольного натурального числа r рассмотрим последовательность рациональных чисел l / r, 2 / r, … ,  r / r. В интервале [0, α] есть ровно [rα] элементов этой последовательности. Теперь посчитаем эти элементы вторым методом. Мы записываем рациональные числа j / r, 1 ≦  j ≦  r, в приведенной форме, а затем подсчитываем для каждого положительного делителя d числа r полученные рациональные числа со знаменателем d, лежащим в [0,α]. Таким образом, мы приходим к тождеству

                                                                (1)

Применяя формулу обращения Мебиуса к (1), получаем

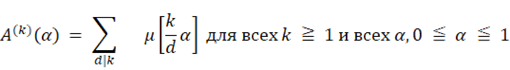
Следовательно, для всех α с 0 ≦  α ≦ 1 имеем

       (2)

Следовательно, D^(k) ≦  (1 / Φ(k)) ∑_d|k|μ(d)| = g(k). Теперь, g(k) - мультипликативная функция теории чисел. Чтобы доказать, что lim_k⟶∞g(k)k^1-∈  = 0 , поэтому достаточно показать, что lim_p8_⟶∞g(p⁸)(p⁸)^1-∈ = 0, где p⁸ пробегает все простые степени. Ноg(p⁸)(p⁸)^1-∈ = 2p^-∈8(1-1/p) ≦ 2p^-∈8, и все готово.

Вернемся теперь к последовательности x₀, x₁, ... , x_Q-1. Поскольку существует примитивный корень по модулю m, мы должны иметь m = 2, 4, p⁸, или 2p⁸, где p - нечетное простое число, а s ≧ 1. Для m = 2 и 4 легко получаем D = ½  и D = ¼, соответственно, для остальных случаев справедливы следующие оценки.

Теорема 2. Если m = р⁸, то D ≦  l/Q. Если m = 2p⁸, то D ≦  2/Q.

Доказательство. Заметим, что последовательность x₀, x₁, … , x_Q-1 пробегает в некотором порядке все рациональные числа i/m с 1 ≦  i ≦ m и НОД (i,m) = 1. Следовательно, A(α) = A^(m)(α), и мы можем применить (2). При m = p⁸ для всех α с 0 ≦  α ≦ 1 получаем

.

Для m = 2p⁸ мы получаем для всех α с 0 ≦  α ≦ 1

Хорошо известно (см., Например, [4]), что невязка D любой последовательности в [0, 1] с Q элементами должна удовлетворять D ≧ ½ Q. Следовательно, никакое существенное улучшение теоремы 2 невозможно. Мы отсылаем к [1] за результатами о распределении псевдослучайных чисел в случае m = 2⁸ с s ≧ 3 (конечно, тогда λ больше не является примитивным корнем).

Из теоремы 2 следует две оценки погрешности численного интегрирования на основе последовательности x₀, x₁, … , x_Q-1. Сначала применим неравенство Коксмы [3], которое утверждает, что для любой последовательности a₀, a₁, … , a_N-1, в [0,1] с невязкой DN и любого подынтегрального выражения / с ограниченной вариацией V(f) на [0,1], есть

Понятие несоответствия обычно определяется в терминах счетных функций относительно полуоткрытых интервалов [0,α), 0 < α ≦ 1. Но легко видеть, что это совпадает с нашим понятием несоответствия, в котором мы использовали счетные функции относительно отрезков [0,α], 0 ≦ α ≦ 1.

Следствие 1. Пусть f - функция с ограниченной вариацией V(f) в [0,1]. потом

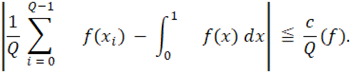
Наконец, применим неравенство, данное автором в [4]: если a₀, a₁, … , a_N-1 последовательность в [0, ]1] с невязкой D_N и f непрерывна в [0,1] с модуль непрерывности ω, то

Для удобства читателя мы прилагаем краткое доказательство. Без ограничения общности мы можем считать, что 0 ≦ a₀ ≦ a₁ ≦ ... ≦ a_N-1 ≦ 1. Тогда мы знаем из [5, уравнение (4)], [6, теорема 1], D_N также определяется формулой

Теперь

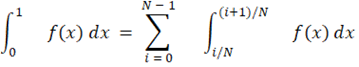
Следовательно

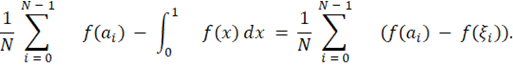
Но |a_i - ξ_i| < max(|a_i - i/N|, |a_i - (i + 1)/N|) ≦ D_N для 0 ≦ i ≦ N - 1 , поэтому |f(a_i) - f(ξ_i)| < ω (D_N) для 0 ≦ i ≦ N - 1, и все готово.

Используя тот факт, что ω- неубывающая функция, приходим к следующему следствию.

Следствие 2. Пусть f - непрерывная функция в [0,1] с модулем непрерывности ω . Тогда

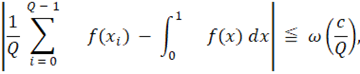
где c имеет то же значение, что и в следствии 1.