Подобия плоскости и их приложение к решению задач

Аннотация. В данной статье рассматривается подобие плоскости, а также применение подобия при решении задач элементарной математики.

Ключевые слова: подобие, гомотетия, преобразование.

Подобием или преобразованием подобия называют преобразование плоскости, для которого  число  такое, что для  и их образов , ,  .

Пример:

1) Так как для  движения , то движение – это подобие с коэффициентом .

2) Гомотетия – это преобразование плоскости, для которого задан центр  и коэффициент , так что произвольная точки  и  . Обозначение .

Пусть 

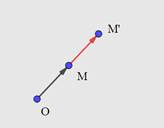
Рисунок 1. Пример при 

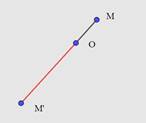
Рисунок 2. Пример при 

Пусть гомотетия  à, à. Тогда по определению получаем:

 (3)

По определению произведение вектора на число получаем:

или   является подобием с коэффициентом подобия .

 Пусть задана . Введём ПСК . 

Рисунок 3. Графическое изображение

По определению  координаты , . Тогда,

  - формула .               

Рассмотрим простейшие свойства .

1) прямую переводит в прямую.

2) сохраняет простое отношение трёх точек,

если , то .

3)  сохраняет величину угла.

4)  сохраняет ориентацию плоскости.

Рассмотрим две подобия  с коэффициентом   и  Пусть 

 . По определению подобия  ,  ⇒

. Следовательно, композиция  – подобие с коэффициентом .

 – подобие с коэффициентом .

Определение. Если преобразование подобия сохраняет ориентацию плоскости, то его называют преобразованием подобия 

В противном случае 

Пусть  – подобие с коэффициентом  Введём ПСК  . Тогда, 
 – формулы подобия с коэффициентом в ПСК.

если  подобие ,

, если  подобие 

Если задана преобразование плоскости 
 – где  то оно есть преобразование подобия с коэффициентом .

При  – подобие ,  подобие 

Задача 1. Диагонали ромба  пересекаются в точке . Отрезок -перпендикуляр, проведенный к стороне . Вычислить длину стороны ромба, если .

Решение:

∆ подобен ∆, так как .
Тогда мы можем составить пропорцию

см                            Ответ: 8см.

Задача 2. В прямоугольном треугольнике  угол см,  – высота, . Найдите 

Решение:

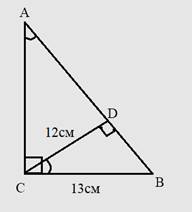
Рисунок 4. Иллюстрация к задаче 2

1) 

 – прямоугольный, по теореме Пифагора  см.

2) 

 см.

3)  – прямоугольный, 

см.

Ответ: 5см, 31,2см.

Задача 3.  Две окружности  и  касаются внутренним образом в точке  В произвольной точке  внутренней окружности проведена к ней касательная, отрезок  которой, заключенный внутри внешней окружности, делится этой точкой на два отрезка  и . Докажите, что оба эти отрезка видны из точки  касания окружностей под равными углами.

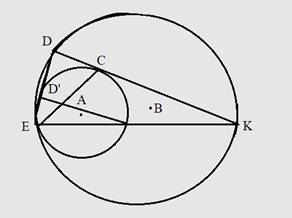
Рисунок 5. Иллюстрация к задаче 3

Доказательство. Заданные окружности на плоскости определяют две гомотетии. Рассмотрим гомотетию с центром в точке  и парой соответствующих точек и . При этой гомотетии вторая окружность перейдёт в первую, прямые  и  отображаются в себя, а точка  и соответствуют точки  и  на первой окружности. Гомотетичные прямые  и  параллельные между собой. Но если касательная параллельна к хорде, то она делит дугу, стягиваемую этой хордой, пополам. Отсюда следует, что угол  и  равны как вписанные углы, опирающиеся на равные дуги.