Объединяющая теория
Журнал: Научный журнал «Студенческий форум» выпуск №3(3)
Рубрика: Физико-математические науки

Научный журнал «Студенческий форум» выпуск №3(3)
Объединяющая теория
Введение
Ещё в 1864-м году в статье «Динамическая теория электромагнитного поля», Д.К. Максвелл впервые сформулировал понятие электромагнитного поля как физической реальности, имеющей собственную энергию и конечное время распространения, определяющее запаздывающий характер электромагнитного взаимодействия [5], заявив о неразделимости природы электрического и магнитного полей. В 1874-м году Н.А. Умов ввёл представление о потоке энергии в пространстве, без конкретизации её физической природы. В 1884-м году Д.Г. Пойнтинг разработал идеи Умова и применил их к электромагнитному полю, получив выражение для вектора плотности потока электромагнитной энергии [1]. После, предложенная в начале XX века А. Эйнштейном общая теория относительности (ОТО) утверждала: «скорость передачи причинного взаимодействия конечна и не может превышать скорость света в вакууме [3]», что было подтверждено экспериментально 11.02.2016 при открытии гравитационных волн [4]. Отсюда напрашивается вывод, что всё наблюдаемое в нашей вселенной имеет электромагнитную природу, а значит и частицы должны иметь электромагнитную природу, что вполне логично для заряженных частиц.
Предположение 1. Геометрическое описание частиц
Предположим: частицы, имеющие заряд, существуют продолжительное время за счёт замкнутой конфигурации (рис.1) вектора Умова-Пойнтинга, ![]() – плотности потока энергии электромагнитного поля , что не даёт частице терять энергию.
– плотности потока энергии электромагнитного поля , что не даёт частице терять энергию.
![]()
где: ![]() – вектор напряжённости электрического поля,
– вектор напряжённости электрического поля, ![]() – вектор напряжённости магнитного поля.
– вектор напряжённости магнитного поля.
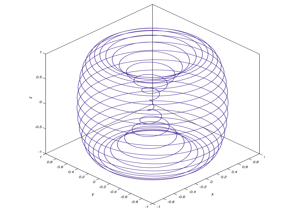
Рисунок 1. Конфигурация замкнутого вектора плотности потока энергии электромагнитного поля
Рассмотрим сечение, проходящее через ось ![]() , поверхности, образованной вращением данной кривой относительно оси
, поверхности, образованной вращением данной кривой относительно оси ![]() , и преобразованной в эквивалентную фигуру – тор (рис. 2), зададимся направлением вектора
, и преобразованной в эквивалентную фигуру – тор (рис. 2), зададимся направлением вектора ![]() относительно
относительно ![]() по часовой стрелке. На рисунке 2:
по часовой стрелке. На рисунке 2:
· ![]() – проекция составляющей воктора Умова-Пойнтинга, перпендикулярной сечению,
– проекция составляющей воктора Умова-Пойнтинга, перпендикулярной сечению,
· ![]() – проекция составляющей воктора Умова-Пойнтинга, лежащей в плоскости сечения,
– проекция составляющей воктора Умова-Пойнтинга, лежащей в плоскости сечения,
· ![]() – вектор напряжённости магнитного поля, порождённый
– вектор напряжённости магнитного поля, порождённый ![]() ,
,
· ![]() – вектор напряжённости магнитного поля, порождённый
– вектор напряжённости магнитного поля, порождённый ![]() ,
,
· ![]() – вектор напряжённости электрического поля,
– вектор напряжённости электрического поля,
· О – ось симметрии сечения,
· ![]() – округлая ось, образованная центрами окружностей сечения тора.
– округлая ось, образованная центрами окружностей сечения тора.
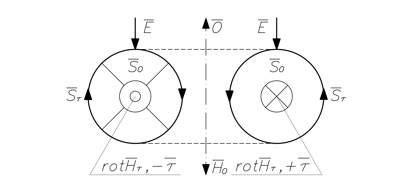
Рисунок 2. Сечение, проходящее через ось ![]() , поверхности, образованной вращением кривой относительно оси
, поверхности, образованной вращением кривой относительно оси ![]()
Предположение 2. Пространственное расположение геометрии частиц
Рассмотрим формулу силы электростатического взаимодействия заряженных частиц:
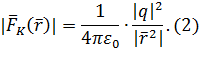
Известно, что данная функция описывает эквипотенциали в форме концентрических сфер. Выберем сферу произвольным радиусом ![]() и проинтегрируем напряжённость по этой поверхности:
и проинтегрируем напряжённость по этой поверхности:
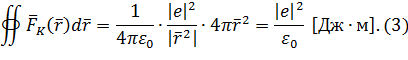
Полученное выражения (3) обозначим ![]() и назовём энергоёмкость системы, так как очевидно, что данная величина является константой для частицы.
и назовём энергоёмкость системы, так как очевидно, что данная величина является константой для частицы.
Разделим размерность выражения (3) на размерность выражения (1):
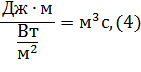
полученная размерность имеет 4-ю степень, т.е. описывает 4-мерные объекты, отсюда предположим:
· конфигурация вектора ![]() , представленная на рисунке 1 располагается в 4-мерном пространстве-времени, а его сечение описанное на рисунке 2 – в 3-мерном;
, представленная на рисунке 1 располагается в 4-мерном пространстве-времени, а его сечение описанное на рисунке 2 – в 3-мерном;
· обязательное наличие 2-х сечений данной конфигурации вектора плотности потока энергии ![]() с разным направлением его вращения в пространстве объясняет феномен «квантовой запутанности».
с разным направлением его вращения в пространстве объясняет феномен «квантовой запутанности».
Описание элементарных частиц
Протон (от др.-гр. ![]() – первый) – рисунок 3, где
– первый) – рисунок 3, где ![]() – вектор Умова-Пойнтинга,
– вектор Умова-Пойнтинга, ![]() – вектор напряжённости электрического поля,
– вектор напряжённости электрического поля, ![]() – вектор магнитного момента.
– вектор магнитного момента.
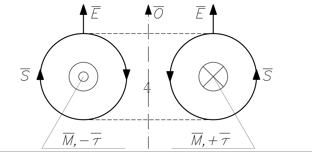
Рисунок 3. 2-мерная интерпретация 3-мерного сечения 4-мерного протона, пересекающего наше пространство-время
Сечение протона с учётом квантовой хромодинамики – рисунок 4.
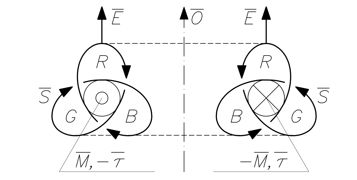
Рисунок 4. 2-мерная интерпретация 3-мерного сечения протона, с учётом квантовой хромодинамики
Упрощённые интерпретации сечений протона, нейтрона и электрона – элементарных частиц, с учётом квантовой хромодинамики представлены на рисунке 5.
Уточним некоторые моменты:
· направление вращения вектора ![]() указано стрелками, левое сечение – по часовой, правое – против;
указано стрелками, левое сечение – по часовой, правое – против;
· вращение вектора происходит в направлении ![]() ;
;
· границы пространств![]() отмечены толстыми линиями;
отмечены толстыми линиями;
· переходы вектора ![]() через эти границы осуществляется при участии мезонов, происходит обмен лептонным зарядом (доменом) между соседними пространствами,
через эти границы осуществляется при участии мезонов, происходит обмен лептонным зарядом (доменом) между соседними пространствами,
· тонкими линиями обозначены каналы слабого взаимодействия, реализуемого через посреднические ![]() и
и ![]() – бозоны.
– бозоны.
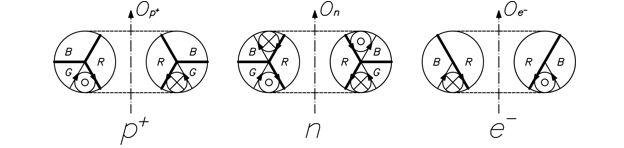
Рисунок 5. Упрощённые точные сечения элементарных частиц с учётом квантовой хромодинамики
Синтез частиц
На основе полученной модели элементарных частиц, синтезируем дейтерий, т. е. ядро, содержащее один протон и один нейтрон. Из рисунка 6 видно, что для синтеза необходим мезон, в данном случае ![]() -мезон.
-мезон.
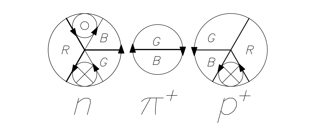
Рисунок 6. Синтез ядра дейтерия
Теперь синтезируем водород, т.е. атом содержащий один электрон и один протон. Из рисунка 7 видно, что для синтеза необходим фотон.
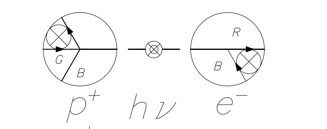
Рисунок 7. Синтез атома водорода
Теперь синтезируем нейтрон, т.е. объединим протон и электрон. Из рисунка 8 видно, что для синтеза необходимо нейтрино, в данном случае электронное анти-нейтрино (приставка анти- означает обратное направление вращения вектора ![]() в сечении частицы).
в сечении частицы).
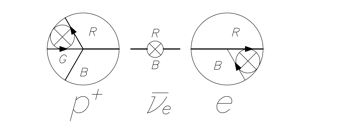
Рисунок 8. Синтез нейтрона
Результат синтеза частиц можно описать векторным произведением синтезирующих частиц, например синтез дейтерия (рис. 9). При этом, для синтеза частиц, расположенных на побочной оси, необходим ![]() -мезон, а для синтеза частиц, расположенных на главной диагонали – нет, но необходимо изменение их спина, значит, синтез частиц есть векторное перемножение проекций вектора
-мезон, а для синтеза частиц, расположенных на главной диагонали – нет, но необходимо изменение их спина, значит, синтез частиц есть векторное перемножение проекций вектора ![]() частиц на ортонормированные оси пространства количества частиц.
частиц на ортонормированные оси пространства количества частиц.
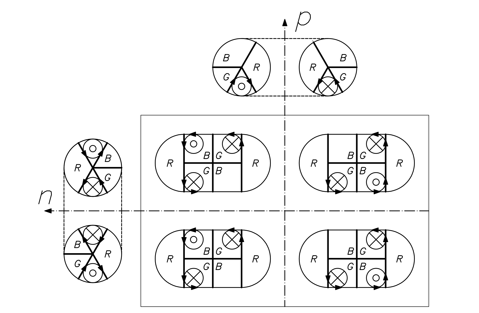
Рисунок 9. Матрица синтеза дейтерия
Ортонормирование пространств модели
Для начала оставим плоскую карту ядерных взаимодействий (рис. 10).
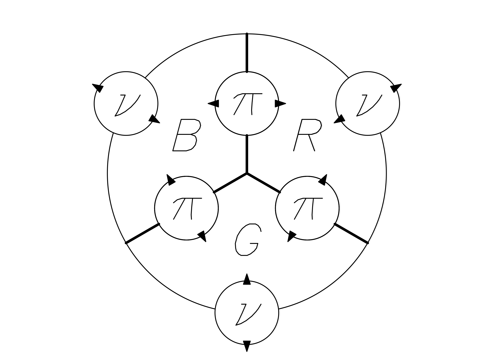
Рисунок 10. Карта ядерного взаимодействия
На основе информации из [6] составим таблицу частиц трёх поколений (табл. 1).
Таблица 1.
Роды и поколения частиц
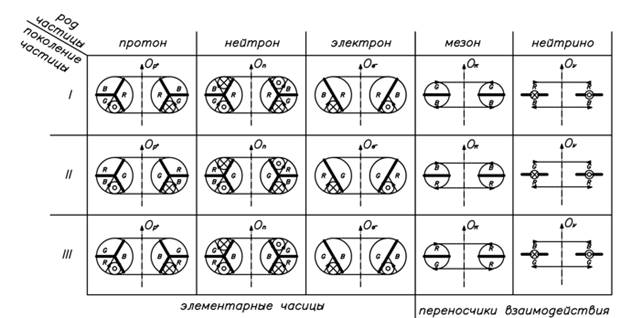
Ортонормируем пространства с учётом их взаимодействия, составим плоскую карту превращений частиц (рис. 11).
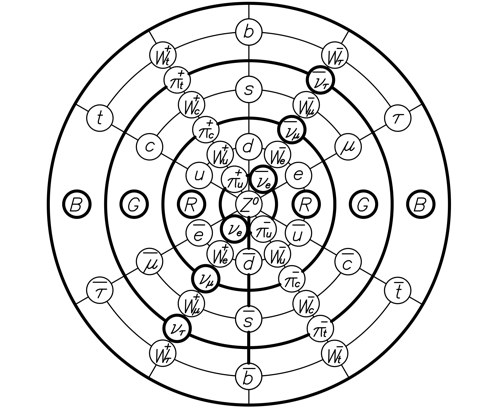
Рисунок 11. Карта превращений частиц
Руководствуясь закономерностями взаимодействий данной модели, можно сделать следующие выводы:
· кварки типа «u» – сегмент траектории вектора плотности потока энергии ![]() , проходящий по границе сечения без лептонного домена, отмеченного окружностью с касательной и указанным направлением вектора;
, проходящий по границе сечения без лептонного домена, отмеченного окружностью с касательной и указанным направлением вектора;
· кварки типа «d» – сегмент траектории вектора плотности потока энергии ![]() с лептонным доменом;
с лептонным доменом;
· высшие поколения кварков образованы при участии частиц больших энергий, что позволяет им переносить лептонные домены в следующее по направлению ![]() пространства;
пространства;
· малые времена жизни высших кварков обусловлены истечением избыточной энергии в пространство через R;
· так как пространства ![]() имеют общую границу, а нейтрино пересекает сечение на границе соседних пространств, то нейтрино может беспрепятственно проходить через их общую точку и менять своё поколение;
имеют общую границу, а нейтрино пересекает сечение на границе соседних пространств, то нейтрино может беспрепятственно проходить через их общую точку и менять своё поколение;
· вращение вектора частиц происходит в направлении ![]() , а античастиц –
, а античастиц – ![]() ;
;
· фотон – вектор плотности потока энергии ![]() , «прыгающий» по 3-мерному пространству c частотой
, «прыгающий» по 3-мерному пространству c частотой![]() в направлении
в направлении ![]() , вектор
, вектор ![]() – перпендикулярен пространству и сонаправлен с
– перпендикулярен пространству и сонаправлен с ![]() испустившей его частицы, при этом
испустившей его частицы, при этом ![]() лежит в пространстве и колеблется с частотой
лежит в пространстве и колеблется с частотой![]() ;
;
· глюон – область вектора ![]() , проходящая через границу соседних пространств;
, проходящая через границу соседних пространств;
· калибровочные W бозоны – частицы, содержащие в себе частицу и античастицу-переносчик.
· калибровочные Z бозоны – частицы, содержащие в себе частицу и античастицу.
Предположение 3. Математическое объединение взаимодействий
Опишем частицы как вращающийся вектор ![]() по границе 3-мерного сечения, при этом вектор
по границе 3-мерного сечения, при этом вектор ![]() совершает полный оборот за время
совершает полный оборот за время ![]() .
.
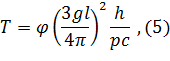
где: ![]() – угол полного оборота,
– угол полного оборота, ![]() – g-фактор,
– g-фактор, ![]() – орбитальное число.
– орбитальное число.
Введём величину:
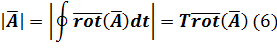
· энергосодержание системы ![]() .
.
Предположим: В силу закона сохранения энергии закона и аддитивности её форм:
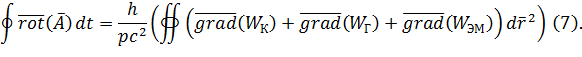
Назовём выражение (7): уравнение неразрывности потока поля энергосодержания системы ![]() в интегральном виде, где:
в интегральном виде, где:
· ![]() – градиент энергии поля электрослабого взаимодействия;
– градиент энергии поля электрослабого взаимодействия;
· ![]() – градиент энергии поля сильногравитационного взаимодействия;
– градиент энергии поля сильногравитационного взаимодействия;
· ![]() – градиент энергии поля координатноимпульсного взаимодействия.
– градиент энергии поля координатноимпульсного взаимодействия.
Перепишем выражение (7) в дифференциальном виде, подставив выражение энергий для частицы и раскрыв интегралы в правой части:
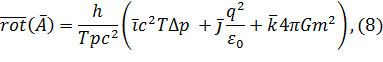
где: ![]() – базисные векторы.
– базисные векторы.
Теперь выразим ![]() для частиц:
для частиц:
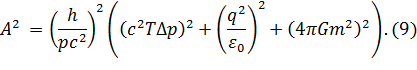
Модель вселенной
Получив выражение для ![]() в пространстве размерностью 5, аналогом 3-мерного сечения – энергии
в пространстве размерностью 5, аналогом 3-мерного сечения – энергии ![]() такого пространства является замкнутая кривая, а аналогом 4-мерного –
такого пространства является замкнутая кривая, а аналогом 4-мерного – ![]() – площадь сечения (рис.12).
– площадь сечения (рис.12).
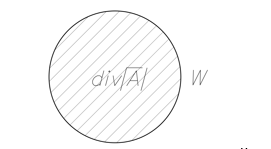
Рисунок 12. Плоский аналог 4-мерного сечения 5-мерной вселенной
Перетекание энергий между параллельными 4-мерными сечениями 5-мерного пространства поля энергосодержания кратно ![]() , и происходит за счёт 4-мерных дыр, значит мы будем наблюдать следующую картину – рисунок 13, на котором изображены соседние 4-мерные параллельные сечения 5-мерного пространства.
, и происходит за счёт 4-мерных дыр, значит мы будем наблюдать следующую картину – рисунок 13, на котором изображены соседние 4-мерные параллельные сечения 5-мерного пространства.
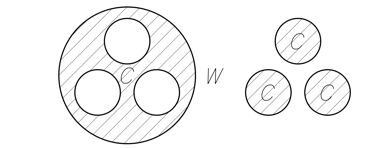
Рисунок 13. Плоский аналог соседних 4-мерных сечений 5-мерного пространства
Получается, 4-мерное сечение 5-мерной вселенной фрактализуется, отсюда:
· фрактализация 4-х мерного пространства в 3-мерном проявляется как увеличение объёма – расширение вселенной;
· фрактализация пространства осуществляется за счёт образования чёрных дыр, через которые энергия перетекает в параллельное подпространство;
· рождение дыры сопровождается рождением новой вселенной в параллельном 4-мерном пространстве;
· тёмная материя – материя, расположенная в параллельном нашему пространстве;
· тёмная энергия – энергия, перетекающая в наше пространство из параллельного надпространства.
Заключение
Данная модель объединяет в себе такие модели, как: стандартная модель, СТО, ОТО, 11-мерные суперструны. Более того, описывает явления, не описанные стандартной моделью, такие как квантовая запутанность и нейтринные осцилляции, объясняет природу массы частиц и многое другое.
Список литературы:

