Математическая модель описания системы надежности функционирования парового котла ТГМ-96Б с использованием избыточной информации первичных преобразователей

Аннотация. Надежность – это способность объекта выполнять осуществлять свое функционирование определенное количество времени в заданных режимах работы. Работа любого объекта не возможна без определенной оценки надежности. В данный момент времени в связи с развитием работы тепловых электростанций возникает необходимость внедрения совершенных систем обеспечения надежности работы объектов энергетики, таких как паровой котел.

Все существующие системы обеспечения надежности имеют ряд недостатков, которые необходимо исключить в создании более совершенной системы надежности.

Ключевым элементов в создание системы надежности объектов энергетики будут являться первичные преобразователи, отвечающие за функционирования объектов. Каждый из таких первичных преобразователей способен не только осуществлять измерения, но также предоставлять нам информацию о работе объекта, такая информация называется избыточной.

Ключевые слова: Автоматизация; система надежности; паровой котел; математическая модель; первичные преобразователи.

Перед тем как рассматривать математическую модель, определим, что же представляет собой математическая модель описания. Математическая модель — приближенное описание объекта моделирования, выраженное с помощью математической символики.

В данной работе по повышению надежности функционирования парового котла с помощью измерительных блоков ячеек измерительных приборов необходимо описать математическую модель, которая наглядно показывала взаимосвязь связанных между собой измеряемых величин. Проведем определение зависимости блоков ячеек измерительных приборов, на основе работы барабана парового котла.

Уровень в барабане котла является важнейшим измеряемым значением. Его отклонения может привести к аварийным ситуациям. В барабане котла (рисунок 1) присутствуют, входящий поток питательной воды, расход воды из барабана на продувку, а также расход насыщенного пара [2. c. 95].

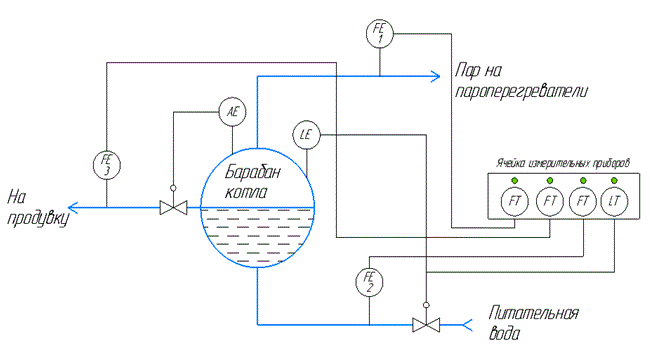
Рисунок 1. Схема блоков-ячеек измерительных преобразователей барабана парового котла

Данная схема показывает ячейку измерительных прибор с взаимосвязанными приборами. Допустим во время работы барабана котла возникает ситуация, когда значение расходомера, FE 2 на трубопроводе подачи питательной воды, показывает высокие значение близкие к аварийному или выше диапазону изменения расхода питательной воды. При возникновении такой ситуации обычно происходит блокировка питательной воды поступающей в барабан котла, продувки, а также насыщенного пара из барабана котла, а также полной остановка работы парового котла. Но что, если проблема не в технологическом процессе, а в отказе расходомера FE 2. Данная ситуация приведёт к ненужным затратам. Для предотвращения таких моментов, необходимо внедрить систему с повышенной надежностью АСУ ТП с использованием избыточной информации первичных преобразователей. При использовании это системы, оператор обращается к блоку ячейке измерительных преобразователей, где показаны значения связанных параметров. Т.е. в случае, когда расходомер FE 2 показывает высокие значения, оператор смотрит значения в блоке-ячейки измерительных преобразователей барабана парового котла, таких как уровень в барабане, расход продувки и расход пара, если все эти значения показывают нормированные показано, то можно судить об отказе расходомера FE  2.

Для того, чтобы иметь наглядное представление зависимости расходов от уровня в барабане котла, необходимо представить математическую модель зависимости. Чтобы найти зависимость между связанными параметрами необходимо предоставить математическую модель описания.

Так как барабан котла — это замкнутая система, она подчиняется закону сохранения массы, т.е. материальный баланс. Закон сохранения масс веществ заключается в том, что во всякой замкнутой системе масса вещества остается постоянной, независимо от того, какие изменения претерпевают вещества в этой системе. Применительно к расчету материального баланса какого-либо процесса производства этот закон принимает следующую простую формулировку: масса исходных продуктов процесса должна быть равна массе его конечных продуктов [1, c.148].

Следовательно, когда производится материальный расчет процесса, необходимо учитывать массу каждого компонента, поступающего в данный аппарат (приход) и массу каждого компонента, уходящего из аппарата (расход). Сумма приходов компонентов должна быть равна сумме расхода, независимо от состава продукта при поступлении и выходе, т.е. независимо от того, каким изменениям они подверглись в данном аппарате [3, c. 38].

Материальный баланс для пароводяного тракта парового котла описывается уравнением:

,                                                                                           (1)

где F_{пит.воды} – расход питательной воды, подаваемой в котел; F_пара – расход производимого пара; F_{продувки} – расход продувочной воды и барабана котла для удаления накапливаемых там солей жесткости.

Для нахождения зависимости уровня жидкости в аппарате L от величины F_{пит.воды,} F_пара, F_{продувки.} Составим уравнение материального баланса аппарата:

,                                                                                     (2)

где V — объем жидкости в аппарате, м3; t — время, с. Отсюда скорость изменения объема жидкости в аппарате:

                                                                                            (3)

Скорость изменения уровня жидкости L, если площадь горизонтального сечения аппарата А (в м2) неизменна по:

                                                                                           (4)

Таким образом, скорость изменения уровня в резервуаре пропорциональна разности потоков жидкости на входе и выходе. Уровень жидкости принимает постоянные значения во времени (скорость =0) только при отсутствии рассогласования потоков F_{пит.воды,} F_пара, F_{продувки}.

Проинтегрируем уравнение (4) в пределах от 0 до t:

                                                                                    (5)

Следовательно, выходная величина объекта пропорциональна интегралу от изменения его входных величин.

При ступенчатом изменении нагрузки объекта на величину ΔF уровень жидкости L изменяется по зависимости:

                                                                                                             (6)

Как следует из уравнения (6), скорость изменения выходной величины при ступенчатом возмущении ΔF постоянна и равна:

                                                                                                                  (7)

Исходя из уравнения (7) последнего уравнения определяется зависимость уровня в барабане котла от входящих и исходящих потоков. На основе этого можно говорить, о правильности использования блоков ячеек измерительных приборов, которые имеют взаимосвязь между измеряемыми параметрами.