Анализ факторов, влияющих на результаты теплового анализа методом конечных элементов

Аннотация. В работе рассмотрены факторы, влияющие на результаты анализа тепловых режимов работы электромеханических преобразователей методом конечных элементов.

Ключевые слова: моделирование, электромеханический преобразователь, метод конечных элементов, тепловой анализ.

При разработке электрических машин еще на ранней стадии проектирования возникает необходимость в расчете и моделировании электромагнитных, тепловых и механических задач. Температурный анализ играет заметную роль. Как правило, интерес представляют распределение температуры, температурного градиента и теплового потока. Надежность проводов электрической машины в значительной степени определяет ее общую надежность. Доля отказов из-за повреждения обмоток для асинхронных двигателей мощностью более 5 кВт составляет 85-95%, при этом около 50 % отказов вызывается эксплуатационными причинами, которые в большинстве случаев приводят к перегреву обмоток. Убытки от выхода из строя обмоток могут составлять до 80% от стоимости годового выпуска электрических машин. Эти обстоятельства приводят к выводу о необходимости достаточно подробного рассмотрения выбора проводов обмоток [1].

Прогнозирование теплового состояния электрической машины на этапе ее проектирования осуществляется посредством метода конечных элементов (FEM). Этот метод является основой системы инженерного анализа (САЕ) и доступен не только специалистам – профессионалам, но входит в разряд обычных инструментов инженеров – проектировщиков и исследователей [2].

FEM – один из наиболее гибких и универсальных методов решения широкого круга задач механики сплошной среды, тепло-, электро- и магнитостатики и многих других задач науки и техники.  CAE – система ELCUT позволяет решать двумерные краевые задачи математической физики, описываемые эллиптическими дифференциальными уравнениями в частных производных относительно скалярной или однокомпонентной векторной функции (потенциала), а также задачи расчета напряженно-деформированного состояния твердого тела [3].

При моделировании тепловых задач возникает вопрос оценки факторов, влияющих на достоверность распределения температуры в исследуемом объекте. В данной работе проводится анализ этих факторов на примере поперечного сечения электрической машины, показанной на рис.1. На рисунке для упрощения не показаны магниты на роторе. В идеальном случае в каждом пазу необходимо поместить сечения всех витков с изоляцией. Однако в этом случае сетка конечных элементов оказывается слишком плотной, что приводит к невозможности расчета из-за большого числа узлов. Поэтому все витки в реальном объекте заменяются n эквивалентными проводниками [4]. Суммарная площадь, занимаемая неизолированным проводом в каждом полупазе, может быть вычислена по формуле (1):

,                                                                                                     (1)

где S_э - площадь полупаза, k_зп - коэффициент заполнения медью (k_зп ≈0.3-0.4).

В свою очередь эквивалентные проводники могут быть круглыми или вытянутыми, образованными прямоугольной областью с двумя полуокружностями на концах. В этом случае суммарная площадь  S_э примет вид:

                                                                                         (2)

Где  n - число эквивалентных проводников, d_э- диаметр эквивалентного проводника,   k_в - коэффициент вытянутости проводника (изменяется в диапазоне от 0 до 4, в зависимости от формы проводника). Тогда диаметр эквивалентного проводника находится из (3).

                                                                                                 (3)

Далее в каждом полупазе геометрической модели равномерно размещаются эквивалентные проводники с диаметром d_э. Примеры их размещения показаны на рис. 1 и 2. Для каждого элемента модели задаются коэффициенты теплопроводности λ (Вт/(К*м).

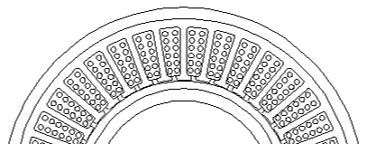
Рисунок 1 . Объект моделирования при заданном числе эквивалентных проводников n=6  и k_в=0

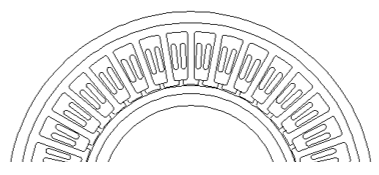
Рисунок 2 . Объект моделирования при заданном числе эквивалентных проводников n=1 и k_в≠0

Теплопередача осуществляется тремя способами: теплопроводностью, конвекцией и тепловой радиацией. Моделирование теплопередачи в ELCUT учитывает только теплопроводность. Другие механизмы – конвекция и радиация – могут быть учтены в виде граничных условий, описывающих взаимодействие конечно-элементной модели с внешней средой и объектами. В рассматриваемой модели задавались два граничных условия 3-го рода на наружном и внутреннем ребрах:

• условие плотности конвективного потока 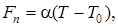 где α - коэффициент конвекции (Вт/(м²·К)), T₀ = 293 K (20°С) - температура окружающей среды.

• условие радиации , где β- коэффициент поглощения поверхности (β=0,85); k_SB- константа Стефана-Больцмана; T₀=293 K - температура окружающей среды.

Постоянное значение тепловой нагрузки в эквивалентных проводниках за счет протекания тока задавалось в виде объемных плотностей тепловыделений (Вт/м³).

Целью вычислительных экспериментов является исследование следующих факторов, влияющих на среднюю температуру в пазу:

• число эквивалентных проводников;
• значения коэффициентов теплопроводности изоляции и магнитопроводов;
• значения коэффициентов конвекции.

Если для проводников из меди коэффициент теплопроводности имеет вполне определенное значение, то для изоляции, заполняющей паз в модели, этот коэффициент может иметь значение в некотором диапазоне. Это объясняется тем, что под понятием «изоляция» в данном случае подразумевается совокупность изоляции собственно проводников (витков), пазовой изоляции и компаунда. В общем случае каждый из указанных видов изоляции имеет свой коэффициент теплопроводности. Для задания коэффициента теплопроводности изоляции берется некоторый усредненный коэффициент. Если в действительности такой усредненный коэффициент будет больше, чем задан в модели, то температура в эквивалентных проводниках (именно там она максимальна) снизится. Но, если на самом деле, коэффициент теплопроводности ниже, то увеличение температуры паза неизбежно, что может привести к перегреву электромеханической машины и потере её работоспособности. Использование встроенного в ELCUT средства LabelMover позволяет задать коэффициент теплопроводности для изоляции в широких пределах и оценить изменение температуры (рис.3) [3]. Кривые получены при фиксированных значениях коэффициента конвекции α=4 Вт/(м²·К) и коэффициента теплопроводности магнитопроводов λ=83Вт/(К·м). Из графиков следует, что, действительно, с уменьшением коэффициента теплопроводности, растет температура в проводниках и чем меньше количество эквивалентных проводников, тем выше температура в них. Таким образом, при замене суммарной площади меди одним эквивалентным проводником в модели наблюдается максимальное значение температуры.

Влияние коэффициента теплопроводности магнитопровода статора и ротора показано на рисунке 4.  Кривые получены при фиксированных значениях коэффициента конвекции α=4 Вт/(м²·К) и коэффициента теплопроводности изоляции λ=18Вт/(К·м).

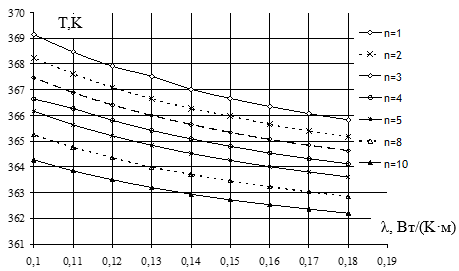
Рисунок 3. Графики зависимости средней температуры в витках от коэффициента теплопроводности изоляции при разном количестве эквивалентных проводников n

Из графиков (рис.4) следует, что с уменьшением коэффициента теплопроводности материала магнитопроводов статора и ротора температура в проводниках растет, но незначительно, в пределах 0,5 градуса.

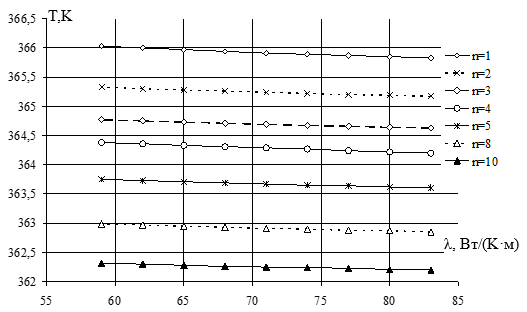
Рисунок 4. Графики зависимости средней температуры в витках от коэффициента теплопроводности материала магнитопроводов статора и ротора при разном количестве

Использование LabelMover в ELCUT также позволяет оценить изменение максимальной температуры при различных значениях граничных условий (рис.5). Кривые получены при фиксированных значениях коэффициентов теплопроводности изоляции λ=18Вт/(К·м) и магнитопроводов λ=83Вт/(К·м). Из графиков (рис.5) следует, что с увеличением коэффициента конвекции уменьшается температура в проводниках, причем величина этих изменений значительна в пределах 20°С. Таким образом, наибольшее влияние на результаты моделирования оказывает неверное задание коэффициента конвекции.

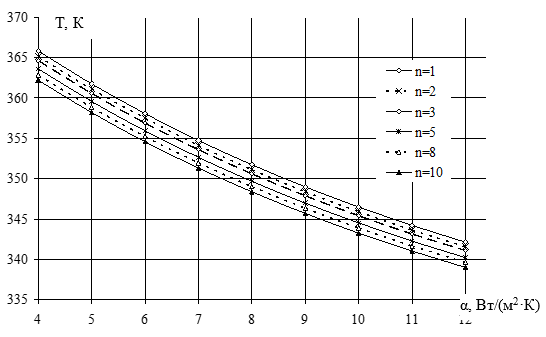
Рисунок 5. Графики зависимости средней температуры по объему в витках от коэффициента конвекции при разном количестве эквивалентных проводников n

Заключение

Таким образом, результаты моделирования тепловых режимов методом конечных элементов на стадии проектирования показали, что следует учитывать факторы, наиболее влияющие на точность результатов, а именно:

• число эквивалентных проводников;
• значение коэффициента теплопроводности изоляции;
• значение коэффициента конвекции.

При задании одного эквивалентного проводника результат моделирования дает максимально возможное значение температуры. На это значение, очевидно, и следует ориентироваться при выборе марки провода.

Влияние изменения коэффициента теплопроводности материала магнитопроводов (электротехническая сталь) на температуру в пазах незначительно.

Наибольшее влияние на максимальную температуру оказывает изменение коэффициента конвекции, поэтому при проектировании следует ориентироваться на его наименьшее значение.