Решение одной математической задачи энергетики

SOLVING A MATHEMATICAL PROBLEM

Victoriya Moseeva

Student of Ulyanovsk aviation  college  - inter-regional center of competences, Russia, Ulyanovsk

Nina Yershova

Master of pedagogical Sciences, teacher, Ulyanovsk aviation college  - inter-regional center of competences, Russia, Ulyanovsk

Аннотация. В статье раскрываются основные понятия метода оптимизации энергетических задач. На конкретном примере энергетической задачи составлена математическая модель задачи и представлен традиционный метод решения. К решению энергетической задачи на оптимизацию применяется транспортный метод решения таких задач.

Abstract. The article reveals the basic concepts of the method of optimization of energy problems. Using a specific example of an energy problem, a mathematical model of the problem is compiled and a traditional solution method is presented. To solve the energy optimization problem, the transport method is used to solve such problems.

Ключевые слова: математическое моделирование, методы оптимизации, энергетическая задача, традиционный метод, целевая функция, искомые переменные, ограничения, граничные условия.

Keywords: mathematical modeling; optimization methods; energy problem; traditional method; objective function; desired variables; constraints; boundary conditions.

Для решения различных профессиональных задач студенту как специалисту необходимы знания основ математического моделирования технических систем, методов расчета и анализа параметров схем замещения системы электроснабжения и рабочего режима, решения оптимизационных задач, современного программного обеспечения персональных компьютеров.

Как правило, математические методы не разрабатываются для решения конкретных задач. Именно поэтому формулировка любой технической задачи должна быть записана с помощью определенных математических выражений. А студент-выпускник должен знать математические методы, предназначенные для решения обобщенных инженерных задач и уметь выбрать целесообразный метод для решения конкретной технической задачи.

Как известно, при выборе оптимального варианта достигается минимальное, максимальное или иное значение какого-то критерия. Этот критерий характеризует качество оптимизации. Для решения задач оптимизации электрическую систему нужно представить в виде математической модели. В математической модели выделяют следующие составляющие:

1) параметры системы, (конфигурация сети, активное и реактивное сопротивление ЛЭП и трансформаторов и т.д.);

2) внешние и внутренние воздействия напряжения, значения электрических нагрузок в различных точках цепи;

3) переменные управления или управляющие воздействия, например, положение точек размыкания;

4) переменные состояния – характеристики режима потокораспределения и т.д.;

5) критерий оптимальности или целевая функция, например, величина потерь мощности или минимум приведенных затрат;

6) ограничения, накладываемые на переменные состояния и переменные управления – это уровни напряжения и допустимые токи нагрузки.

Следует отметить, что математическое программирование представляет собой многократно повторяющуюся вычислительную процедуру, приводящую к искомому оптимальному решению. Выбор метода математического программирования для решения оптимизационной задачи определяется видом зависимостей в математической модели, характером искомых переменных, категорией исходных данных и количеством критериев оптимальности.

Заметим, что решение задач небольшой размерности можно выполнить традиционными вычислениями с помощью калькулятора. Решение же реальных задач, размерность которых может быть достаточно большой, возможно лишь с помощью ЭВМ. Поэтому студент-выпускник должен знать программное обеспечение современных персональных компьютеров и уметь пользоваться этим обеспечением.

Рассмотрим следующую задачу: от трех электростанций мощностью 100 МВт, 25 МВт и 50 МВт энергию потребляют четыре населенных пункта с объемами потребления 60 МВт, 45 МВт, 40 МВт и 30 МВт. Составьте такой план электрических сетей, чтобы все населенные пункты были обеспечены электроэнергией, а общие затраты на передачу электроэнергии были минимальны. Стоимость передачи электроэнергии от первой электростанции до каждого населенного пункта составляет 10, 7, 5, 8 тыс.рублей, от второй электростанции – 3, 6, 8, 4 тыс.рублей, от третьей электростанции – 4, 2, 9, 6 тыс.рублей.

Решим задачу непосредственным вычислением:

Количество переменных: 3х4=12.

Целевая функция: .

По условию задачи .

Система ограничений:

.

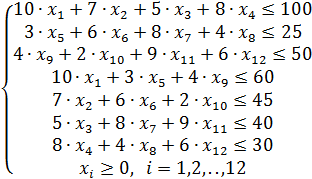Запишем в виде таблицы:

Определим форму записи модели: 

, модель закрытая.

Определим опорный план.

Метод северо-западного угла:

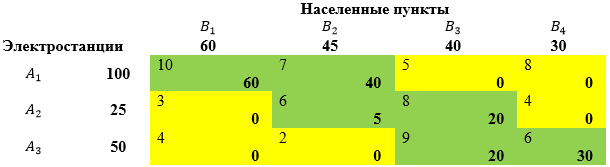
 первая строка закрыта (); первый столбец закрыт ();

 вторая строка закрыта (); второй столбец закрыт ();

 третья строка закрыта.

Значение целевой функции для найденного плана:

 тыс.рублей.

Метод минимальной стоимости:

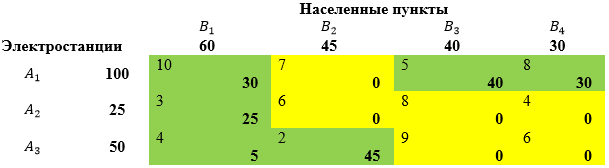
третья строка закрыта (, ); второй столбец закрыт ();

 вторая строка закрыта ();

 третий столбец закрыт, четвертый столбец закрыт, первый столбец закрыт.

Значение целевой функции для найденного плана:

 тыс.рублей.

Метод аппроксимации Фогеля:

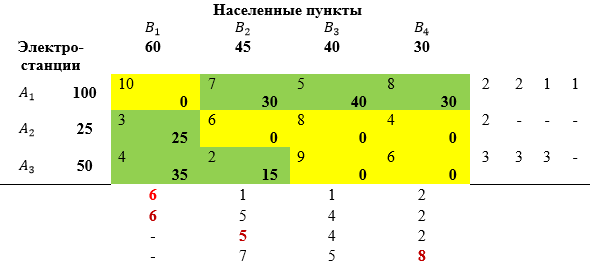
 выбираем первый столбец 

 вторая строка закрыта ();

 выбираем первый столбец 

 первый столбец закрыт ();

 выбираем второй столбец 

 третья строка закрыта ();

 выбираем четвертый столбец  четвертый столбец закрыт;

 третий столбец закрыт; .

Значение целевой функции для найденного плана:

 тыс.рублей.

Лучший результат:  тыс.рублей.

Проверим его на оптимальность методом потенциалов. Составим систему уравнений для каждой заполненной клетки:

, , ,

, , .

Пусть , тогда , , , , , , .

Для каждой свободной клетки вычислим .

,

,

,

,

,

.

Так как все найденные , то найденный план является оптимальным.

Ответ: 

  тыс.рублей.

Получим решение задачи в среде MS Excel

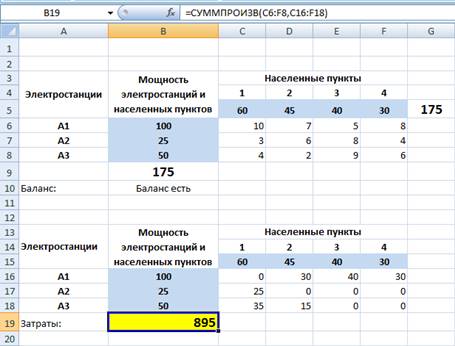
Рисунок 1. Фрагмент эл.листа с условием и решением задачи

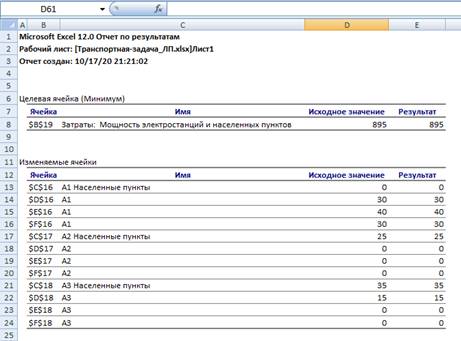
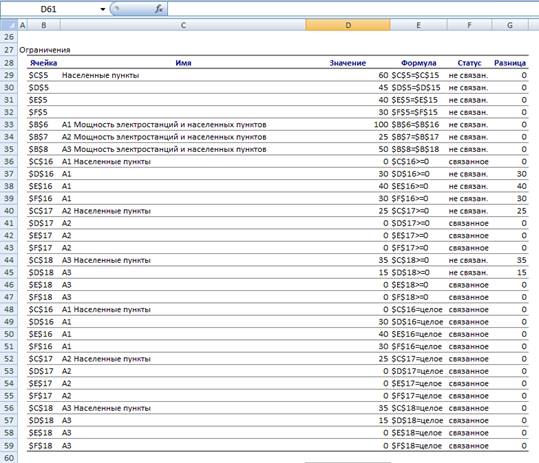
Рисунок 2. Отчет по результатам решения