Теория вероятности в букмекерской деятельности

Теория вероятностей непосредственно связана с экономикой, маркетингом, рекламой и в целом с любым аспектом жизни людей. Мы сами, не замечая того, ежедневно задумываемся при принятии каких-либо решений о вероятности наступления или наоборот не наступления ряда событий. Например, часто люди задаются вопрос пойти или нет на прогулку, на занятия и так далее. А вопросы «Быть или не быть?», «Делать или нет?», «А вдруг повезет?» сопровождают людей на протяжении всей их жизни, люди всегда надеются на судьбу или на чудо, однако они даже не осознают, что находятся под властью такой науки, как теория вероятности. А значит все мы можем посчитать действие того или иного события, обладая определенными теоретическими знаниями.

Таким образом, именно понятиями и инструментами теории вероятностей оперируют люди во многих сферах своей деятельности, вычисляя вероятность наступления интересующего события, делая определенные выводы, тем самым получая возможность принимать обоснованные управленческие решения.

Нас заинтересовала эта тема, и мы захотели разобраться в ней, ведь теория вероятности играет роль отличного инструмента, правда только в руках умелого пользователя. Поскольку именно возможность грамотно просчитать все возможные ходы и суметь прогнозировать будущее может сделать из самого простого вчерашнего студента востребованного бизнесмена, экономистом, маркетологом и т.д.

В данной статье мы хотим рассмотреть роль теории вероятностей в букмекерской деятельности.

Мы решили разобраться действительно ли выигрыш — это всегда магия и судьба, может быть когда-то и кем-то, нам было предписано выиграть большую сумму? Или может это базовый механизм, разгадав который можно приструнить удачу? Математика в ставках имеет большое значение. На этой науке построен весь букмекерский бизнес. Нельзя получить прибыль, надеясь на свои догадки. Понимание этой концепции отличает победителя от неудачника, успешного игрока от человека, который регулярно проигрывает свои сбережения в букмекерской конторе. Большинство любителей спортивных пари теряют деньги, а ведь совсем не сложно выделить немного времени и разобраться с основными математическими понятиями в ставках на спорт. Мы решили выяснить: какие же основные показатели влияют на точное знание исхода событий, и как работают законы математики в спортивных ставках.

Первый показатель, о котором мы хотим рассказать, – букмекерские коэффициенты. Это числовой множитель, выражающий вероятность того или иного события в спортивном состязании и включающий маржу букмекера. Коэффициент дает игроку понять, каков потенциальный выигрыш по ставке. Для расчета вероятности с помощью данного коэффициента нужно разделить единицу на выставленный коэффициент.

Например, представим в футбольном матче команда «А» победит с коэффициентом 2,05; ничья 3,6. А победа команды «Б» составит 3,8. Вероятность всех событий составит: победа «А» 49%, ничья 28%, а победа «Б» 26%. Следовательно, вероятнее всего победит команда «А». Но чтобы не высчитывать вероятности при каждой ставке, стоит обращать внимание на меньшее значение коэффициента. Но стоит помнить, что никто не может предсказать исход поединка со стопроцентной точностью. Тем более букмекерские конторы сознательно допускают ошибки в своих предсказаниях, чтобы увеличить свою прибыль.

Следующий показатель – это маржа для букмекера. Простыми словами маржа букмекера – это его страховка от проигрыша, его гарантированный выигрыш. Аналитики в букмекерских конторах рассчитывают вероятность прохода событий и переводят ее в коэффициенты. Вернемся, к примеру, о котором говорили ранее, а точнее рассмотрим тот же матч команд «А» и «Б». Если сложить проценты, которые дает букмекер в коэффициентах, то получим 103%. Эта вероятность больше ста процентов, т.е. 3% составляет маржа, процент за услуги

Так же немало важными показателями являются математическое ожидание и дисперсия в ставках.

Чтобы показать, в чем заключается важность дисперсии в ставках, воспользуемся простым примером с монеткой. Вероятность выпадения орла или решки равна 50% соответственно, но, как известно, на практике такой закон практически никогда не работает, одна из сторон монеты может выпасть очень много раз подряд. Многие букмекеры считают, что каждая проигрышная ставка на событие с 50-процентной вероятностью прохода лишь увеличивает вероятность выигрыша в следующий раз. Так стала очень популярна стратегия Мартингейла, она подразумевает то, что игрок с каждой ставкой будет удваивать сумму ставки от предыдущей, для того чтобы получать прибыль или отыграться. Но в большинстве случаев такой метод приводит к проигрышу и при длительном использовании, как раз из-за дисперсии.

Если рассматривать подобную ситуацию, но уже со стороны математического ожидания, то после выигрыша должен наступить проигрыш и наоборот, но такого не случается и особенно это заметно при небольшом количестве попыток. Математическое ожидание демонстрирует, с какой долей вероятности событие будет выпадать на длинной дистанции (при большом количестве попыток).  Для опытных игроков самое важное это правильно просчитать дисперсию, т.к. это покажет, насколько вероятно выпадет то или иное событие. Так если мы подбросим монетку дважды, то два раза может выпасть орел, а может и решка. В итоге математическое ожидание не всегда подскажет верный исход.  Очень важно в таком деле учитывать как можно больше количество исходов событий, так цифры дисперсии могут показать наиболее точно вероятный исход.

Данную тему статьи мы не можем оставить без внимания методов прогнозирования исходов событий или моделирования ситуаций. На сегодняшний день их существует безмерное количество. Мы хотим остановиться и рассказать более подробно о некоторых из них.

Первый метод, который привлек наше внимание, был метод Монте-Карло.

Это метод моделирования случайных величин с целью вычисления характеристики их распределений. Используется для решения задач в области физики, математики, экономики, теории управления. Данный метод был разработан в прошлом веке, с помощью него можно получить множество результатов, которые напрямую зависят от исходных данных. Любой параметр, который нельзя установить точно, представляется в виде большого множества вариантов. Допустим, в чемпионате по баскетболу соревнуются три команды. До завершения турнира осталось 7 матчей, нужно узнать какова вероятность того, что победит первая команда. Для этого можно использовать метод Монте-Карло, чем больше мы будем знать входных данных, тем точнее будет прогноз, это может быть наличие травм у игроков, состав команды, день в который происходит турнир.

Следующий метод называется байесовская вероятность.

Данная теория была разработана Томасом Байесом, и она гласит, что новые обстоятельства влияют на вероятность того или иного исхода. Эта теория существует в виде формулы:

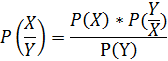
P(X/Y) – это вероятность события X при условии события Y, а P(Y/X) – это вероятность события Y при условии события X

Так, например, можно посчитать с какой вероятностью команда победит в матче в дождливую погоду. Воспользуемся теоремой Байеса, букмекер оценил вероятность победы команды в 60%,  в 20% процентах победных матчей команды был дождь, а его вероятность пойти в данную игру составляет 25% по показаниям гидрометцентра. При расчетах выходит: (60*20)/20=75. То есть большая вероятность победы команды следует в дождливую погоду.

И последний метод, о котором мы хотим рассказать, является цепь Маркова

Это последовательность случайных событий с конечным или счётным числом исходов, где вероятность наступления каждого события зависит от состояния, достигнутого в предыдущем событии. Характеризуется тем свойством, что, при фиксированном настоящем будущее независимо от прошлого, т.е. прошлое никак не может повлиять на возможный исход. Так каждый исход событий индивидуален, при подсчете вероятных событий таким методом, необходимо учитывать только текущее положение дел. Для анализа важны лишь совсем недавние матчи команда, прощающие не больше месяца назад. Если грамотно внедрить данную систему, то финансовая математика будет показывать тенденции к повышению вероятности выигрыша.

Таким образом, наша статья показывает, что этот мир, так или иначе, состоит из математики и непрерывно с ним связан. Что касается такого  момента как выигрыш на ставках, то, как минимум 80% всех выигрышей приходится на точный математический расчет. Поэтому букмекеры уделяют большое время  математическому анализу в составлении прогноза на матч или определения вероятности прохода тех или иных событий. Именно благодаря этому расчету в дальнейшем аналитики в букмекерских компаниях высчитывают коэффициенты. А многие профессиональные бетторы (люди, делающие ставки) соревнуются с букмекерами в анализе матчей и самостоятельно высчитывают для себя вероятность исходов, используя математику. Тем самым, наша статья еще раз доказывает важность знания математики в будущем каждого человека.