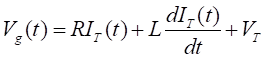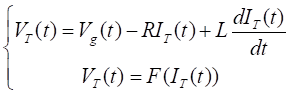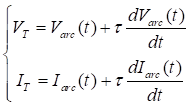Анализ дуговых процессов при размыкании контактов в среде Matlab

При разработке современных, надежных контактных устройств, таких как реле, выключателей, контакторов, пускателей и т.д. необходимо проводить исследования поведения контактов при возникновении электрической дуги. В процессе коммутации электрической нагрузки, при увеличении расстояния между контактами, в межконтактном промежутке коммутирующего устройства вследствие ионизации возникает электрическая дуга. Физически она представляет собой поток заряженных частиц, которые переносятся между контактами.

На рисунке 1 изображена статическая характеристика разряда.  Мы можем разделить эту характеристику на три отличительные области (разделенные пунктирными линиями на рисунке 3.1). Одна область находится между напряжениями -Vd и Vd. Эта область соответствует резистивной части статической характеристики. Разряд в этом случае является тлеющим разрядом или может быть расплавленным мостиком. Поскольку оба являются резистивными, мы отмечаем Rc сопротивление для этой области. Две другие области находятся за пределами напряжений -Vd и Vd и соответствуют дуговому разряду. В этом случае сопротивление дуги является не только простым сопротивлением, но также зависит от тока дуги. Мы отмечаем, что R_arc сопротивление в этих областях. Напряжение Vd - это напряжение отключения, а I_Text - соответствующий ток.

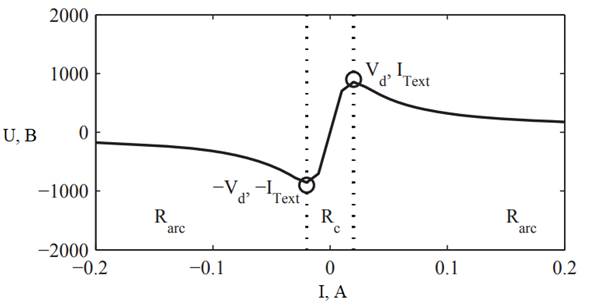
Рисунок 1. Статическая характеристика разряда

Если разряд начинается из-за перенапряжения – это первый тлеющий разряд. Когда напряжение цепи увеличивается, напряжение разряда пересекает напряжение Vd пробоя. Разряд будет таким образом менять площадь, тогда разряд становится дуговым разрядом. При инициировании разряда путем размыкания контакта или использования расплавленного мостика (такого как угольный мостик) в резистивной области вместо тлеющего разряда мы просто имеем сопротивление расплавленного мостика.

В этом случае отмечается сопротивление Rc, потому что оно приводит к той же характеристике, что и на рисунке 1. Таким образом, независимо от того, как инициируется дуга, перед пересечением напряжения разрушения разряд моделируется простым сопротивлением Rc. После пересечения напряжения пробоя разряд моделируется сопротивлением Rarc.

Обычно модели дуги строятся с учетом физики плазмы дуги и редко рассматривают схему, в которой произошла дуга. Такие модели позволяют изучать распределение электронов и ионов, химические реакции и т.д., но не актуальны для инженеров при изучении дуги в электрической цепи.

Модель рассматривает дугу как компонент электрической цепи. Для работы использует ряд простых уравнений, которые позволяют получить точный результат моделирования. Модель основана на уравнениях Варрингтона. В результате исследований им была предложена формула для описания напряжения дуги, в зависимости от тока (формула 1).

Где    Varc –напряжение дуги, В;

Iarc – ток дуги, А;

V0  – электродвижущее напряжение, которое является линейной функцией длины дуги d, В;

P0 – подбираемый параметр, который имеет размерность мощности и является линейной функцией длины дуги d, Вт;

n ­– подбираемый параметр, который зависит от материала электродов (или контактов), используемых для создания дуги. Значение n обычно составляет от 1 до 2.

Для анализа и моделирования в среде Matlab за основу была взята электрическая дуга на постоянном токе. Для данного исследования используется схема ее замещения, представленной на рисунке 2. Данная схема представляет собой соединенные с источником ЭДС резистор и катушку индуктивности.

Рисунок 2. Схема замещения электрической дуги

Моделирование дуги в цепи выполняется с использованием уравнения для напряжения дуги (формула 2), записанного для схемы, приведенной на рисунке 2.

Где    Rg – активное сопротивление схемы замещения, Ом;

Iarc(t) – выражение для тока дуги в цепи в заданный момент времени, А;

Lg – индуктивность схемы замещения, Гн;

Vem – напряжение ЭДС цепи, В.

Для моделирования в среде Matlab необходимо составить уравнение цепи, в которой рассматривается дуга. Рассмотрим простую RL цепь, в которой дуга возникает последовательно (формула 3).

Вторым этапом является вычисление связанной точки поляризации V_T, I_T. Точка поляризации - это точка пересечения между уравнением нагрузки цепи и характеристикой статической дуги. Затем необходимо решить систему уравнений (формула  4).

Система уравнений дает несколько решений для точки поляризации (VT, IT).

В-третьих, используя фильтроподобные уравнения (формула 5) для VT, IT, вычисляются все возможные значения Varc, Iarc.

И выбирается правильное решение Varc, Iarc, используя, сводя к минимуму прогнозируемое изменение мощности ΔP.

Далее был составлен листинг программы, указанный в приложении А.

Промоделировав данный процесс образования электрической дуги при различных скоростях размыкания контактов, были получены графики, указанные на рисунках 3 – 5.

Рисунок 3. Образование электрической дуги при малой скорости размыкания контактов

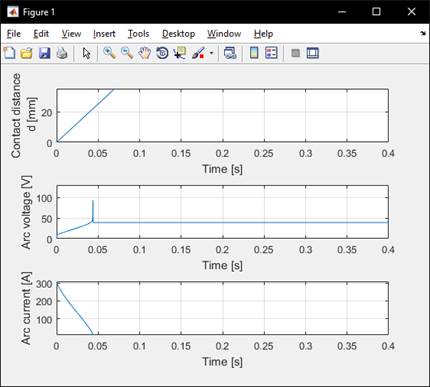
Рисунок 4. Образование электрической дуги при средней скорости размыкания контактов

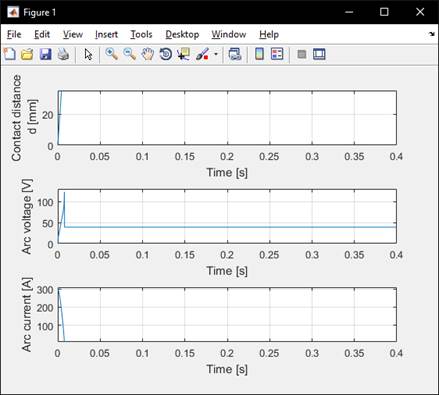
Рисунок 5. Образование электрической дуги при высокой скорости размыкания контактов

Проанализировав данные графики можно сделать вывод о том, что напряжение дугообразования зависит от скорости размыкания контактов.

Исходя из этих графиков видно то, что высокая скорость размыкания способствует высокому напряжению в электрической дуге. Такое напряжение электрическая дуга сказывается, на более сильном разрушении поверхности электрических контактов. Разрушение поверхности приводит к неплотному соединению контактов, вследствие чего данный зазор дополнительному нагреваю площадок.

Поэтому необходимо учитывать индуктивность нагрузки при размыкании контактов, так как она препятствует уменьшению величины электрического тока и ЭДС индукции будет больше, чем ЭДС внешнего источника питания.
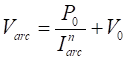