Оптимизация движений многозвенной мехатронной системы

На данный момент большинство мехатронных систем являются многозвенными. Поэтому для их моделирования требуются сложные математические аппараты и программные обеспечения. Любой объект управления требует оптимизированного решения, поскольку любая мехатронная система нуждается в оптимизации, которая позволяет системе решать поставленные задачи в самые короткие сроки и с минимальным потреблением энергии. Создание новой системы начинается с ее моделирования. Поэтому, оптимизация многозвенной мехатронной системы является актуальной проблемой. В данной статье рассматриваются способы решения данной проблемы.

Развитие теории автоматического управления, методов искусственного интелекта, информационных, телекоммуникационных и сетевых технологий, достижения в микросистемной технике, мехатронике и других научно-технических направлениях на рубеже 90-х годов ХХ века вызвали резкую активизацию поисковых исследований и опытно-конструкторских работ по созданию многозвенных мехатронных систем [1].

Переход от теории к практике показал, что наличие в мехатронных системах объектов различной физической природы приводит к тому, что процессы в них характеризуются разнотемповостью, т.е. наличием быстрых и медленных составляющих движения. Кроме того, возможно одновременное присутствие как монотонных, так и медленно затухающих гармонических составляющих [2].

Основная  проблема мехатронных систем связана с сложными взаимодействиями и связями компонентов, которые усложняют интуитивное понимание влияния модификаций параметров. Для эффективного решения этой задачи методы математической оптимизации являются естественными инструментами для разработки методологии логического обоснования для решения этих сложных проблем проектирования.

Синтез оптимальных движений многозвенных систем.

Для синтеза оптимальных законов движения построим динамическую модель многозвенного механизма в параметрической форме на основе введенных кинетического параметра и метрического коэффициента.

Воспользуемся энергетической формой уравнения динамики механических систем, согласно который скорость изменения кинематической энергии равна мощности приложенных сил:

  ,                                                                                                           (1)

Правую часть уравнения (1) представим как скалярное произведение главного вектора силы и вектора скорости концевой точки механической системы:

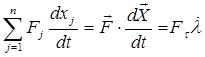                                                                                                   (2)

где  - проекция главного вектора силы на касательную к троектории рабочего органа;  контурная скорость концевой точки.

Левую часть уравнения (1), используя определение кинетического параметра,  можно представить в следующей форме:

                                                                                                                   (3)

Тогда, опираясь на определении метрического коэффициента , уравнение динамики многовенного механизма  (1) приводится к виду [4]

                                     (4)

Оптимизация движений многозвенных мехатронных систем по критерию быстродействия

Для построения оптимальных по критерию быстродействия законов контурного движения воспользуемся полученным уравнением динамики многозвенной мехатронных системы в формуле (3).

Результирующий вектор силы, действующий на рабочий орган, является векторной суммой:

                                                                                                               (5)

где – приведенная к концевой точке сила, развиваемая исполнительными приводами; – вектор внешних сил.

Тогда проекция вектора силы на касательную к троектории рабочего органа является скалярной суммой двух соответствующих компонент:

                                                                (6)

Определим контурное ускорение как производную контурной скорости рабочего органа по времени:

                                                                                               (7)

Предположим, что производная метрического коэффициента существует во всех троектории. Тогда максимальное значение контурного ускорения в заданной точке троектории можно найти по следующей формуле:

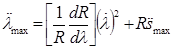                                                                                                   (8)

Метрический коэффициент может быть рассчитан заранее для всех программных троеторий и конфигураци    механической системы. Для расчетов по формуле (8) необходимо знать максимальное параметрическое ускорение _max .

Для определения этой величины обратимся к уравнению динамики (4). Воспользуемся известным соотношением

                                                                                               (9)

где  – вектор обобщенных сил, приложенных в степенях подвижности механизма;   –  матрица Якоби.

Начнем рассмотрение со случая, когда внешние силовые воздействия отсутствуют . В этом случае вектор обобщенных сил для заданного силового воздействия блока приводов находится по формуле

.                                                                                              (10)

  – единичный вектор, наравленный по линии действия силы _M.

Введем специальное обозначение для вектора обобщенных сил, соответствующего единичному вектору силы _M:

                                                                                                             (11)

Следовательно, для силового воздействия с максимальным модулем получаем выражение

                                                                                                               (12)

Величины обобщенных сил, развиваемых исолнительными приводами, ограничены предельными значениями:

                                                                                                      (13)

Если предположить, что проекции вектора положительны, то получим следующую систему ограничений для максимальной силы:

                                                                                                      (14)

Из системы ограничений (9) выбираем граничные значения:

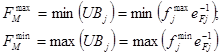                                                                                                    (15)

Полученные выражения дают возможность, найти граничные величины для касательных проекций вектора сил :

                                                                                                 (16)

Таким образом, для расчета необходимо знать направление действия силы относительно заданной троектории, т.е взаимную ориентацию векторов _.

Искомые предельные значения параметрического ускорения для участков разгона и торможения будут иметь вид

                                                                                                          (17)

Если в процессе выполнения технологической операции мехатронная машина имеет силовой контакт с объектом работ, то при синтезе движений исполнительные приводы можно определить по формуле:

                                                                                                                (18)

где ₋ вектор-столбец (n×1) обобщенных сил, обусловленных возмущающим силовым воздействием.

Представим неравенства (13)в следующем виде:

                                                                                               (19)

Оптимизация движений многозвенных мехатронных систем по энергетическому критерию

Одной из наиболее распространенных задач оптимизации движения многостепенных мехатронных систем является синтез по критерию минимума энергетических затрат. Динамические модели на основе кинетического параметра позволяют находить оптимальные движения этого класса наиболее простым и эффективным путем.

Обратимся к определению метрического коэффициента. Из него следует, что энергетически выгодными являются траектории с наибольшим значением R и положительной производной dR/dλ. На таких траекториях при фиксированной величине кинетической энергии рабочий орган достигает большей контурной скорости.

Анализируем оптимизацию движений многозвенных мехатронных систем, выполняющей контурную силовую операцию. В качестве критерия оптимизации выберем величину интерактивной механической энергии, передаваемой от мехатронной машины к объекту работ. Для расчета представим уравнение динамики в энергетической форме:

                                                                                                           (20)

где  –мгновенное значение мощности, развиваемой системой исполнительных приводов;  мгнoвенная интерактивная мощность, обусловленная взаимодействием рабочего органа с объектом работ.

Если не учитывать рассеяние энергии вследствие сил трения, то при фиксированном уровне мощности приводов величина интерактивная мощность будет максимальной , если движение будет происходить при постоянстве кинетической энергии механической системы  C точки зрения динамики изображающей точки это означает потоянство кинетического параметра в процессе движения:

.                                                                                                                (21)

Применив определение метрического коэффициента, получаем для принятого критерия оптимизации следующий закон контурного управления:

.                                                                                                                   (22)

Исходя из этого оптимальный профиль контурной скорости рабочего органа определяется параметрической функцией изменения метрического коэффициента вдоль заданной траектории [3].

Заключение

Оптимизация мехатронных систем довольно сложная задача. Оптимизацию можно производить по критерию быстродействия и по энергетическому критерию. Мехатронные системы, оптимизированные по этим критериям отвечают и современным, и экономическим требованиям.  Исследование оптимизации мехатронных систем имеет важную роль в развитии нашего общества. Проектирование и создание мехотронных систем  является одним из основных ресурсов внедрения нашей республики в число крупных мировых космических держав.