Разработка и программная реализация приложения «Мыльные пузыри»

Столкновение объектов любой природы является одним из актуальных проблем на сегодняшний день. Взаимодействие объектов очень часто используется при разработке физических движков (компьютерных программ, которые выполняют моделирование физических законов реального мира в виртуальном). Физические движки требуют очень больших ресурсов электронных вычислительных систем, так как при моделировании систем необходимо учитывать множество законов физики. Процесс моделирования усложняется (увеличивается количество требуемых ресурсов и времени выполнения моделирования) необходимостью выполнения вычислений в реальном времени.

Наиболее простым способом применения взаимодействия объектов является компьютерная анимация, в котором налагаемые требования на «правдоподобность» ограничиваются восприятием пользователя. Но при этом могут возникнуть значительные отклонения в моделировании столкновений от реальной природы. В итоге можно выделить основную проблему: разработка алгоритма моделирования столкновений, требующего наименьшее число ресурсов, которая не будет допускать ошибок в работе программы.

Для достижения поставленной цели решаются такие задачи, как:

· Ознакомление с физикой удара твёрдых упругих тел;

· Изучение подходов к разработке алгоритмов столкновений;

· Разработка объектной структуры приложения;

· Реализация приложения с графическим интерфейсом пользователя.

Соударение тел

Удар есть процесс взаимодействия тел, движущихся с различными скоростями. Взаимодействие тел происходит в течение очень малого промежутка времени. В классической механике удар считается мгновенным, координаты взаимодействующих тел не меняются, скорости соударяющихся тел изменяются мгновенно [1, с. 41].

Будут рассматривать так называемые центральные удары, при которых точка соударения лежит на прямой, соединяющий центры взаимодействующих тел. Такое допущение возможно в случае, когда рассматриваемые пузыри (тела) являются идеально круглыми.

Удары классифицируются следующим образом:

· По направлению движения соударяющихся тел (прямые и косые);

· По восстановлению недеформированного состояния (неупругие, частично упругие, упругие).

Рассмотрим упругий удар, при котором выполняется закон сохранения импульса: векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.

При упругом столкновении тела с неподвижной плоскостью вектор скорости отражается от плоскости (рис. 1). v1 – вектор скорости до удара, v2 – после удара, причём | v1| = | v2|.

Рисунок 1. Упругий удар тела о неподвижную плоскость

Для обнаружения столкновений объектов существуют апостериорные и априорные алгоритмы.

В первом случае выполняется проверка состояния каждого объекта через небольшие промежутки времени. При таком подходе объекты могут считаться пресекающимися, даже если они оказываются на небольшом расстоянии друг от друга. При выполнении каждой проверки формируется список из пересекающихся объектов, их траектории движения и координат, измененных с учетом факта произошедшего столкновения [2].

Во втором случае для обнаружения столкновений рассчитывается траектория движения тел, позволяющего точно определить момент столкновения.

Апостериорные подход обнаружения столкновений является более простым из двух представленных методов, так как данному алгоритму не приходится обрабатывать большое количество переменных: множество объектов используется в качестве исходных данных, а возвращается подмножество пересекающихся объектов. Преимуществами априорного подхода считаются точность и стабильность. Но возникает трудность в разделении физической составляющей модели от алгоритма обнаружения столкновений.

Структура и программная реализация приложения «Мыльные пузыри»

В программе реализуется класс пузыря, в котором имеются следующие переменные, позволяющие определить текущее положение: координата центра объекта (пузыря), радиус объекта, проекция вектора скорости на оси координат.

Перечислим основные методы, отвечающих за поведение пузырей в процессе выполнения программы. Один из таких методов определяет, находится ли пузырь в состоянии столкновения с другим пузырем (функция, схожая с данным методом определяет столкновение пузыря с границами окна приложения). Следующий метод предназначен для расчета скорости пузырей после их столкновения. Для этого координаты векторов скоростей первого и второго пузырей переводятся в новую систему координат Оx’y’, абсциссой, которой является прямая, соединяющая центры пузырей. Перевод координат происходит с помощью матрицы поворота:

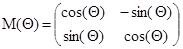
Метод, предназначенный для выполнения анимации движения пузырей, использует стандартный класс QPropertyAnimation, предоставляемый кроссплатформенной средой разработки QtCreator.

Для графического отображения мыльных пузырей используются стандартные библиотеки Qt: QGraphicsScene и QGraphicsView.

Графическое окно приложения представлено на рисунке 2.

Рисунок 2. Графическое окно приложения «Мыльные пузыри»

При тестировании программы не было выявлено явных нарушений работы приложения.

В результате выполнения работы было разработано приложение для моделирования поведения мыльных пузырей при их столкновении