РАЗРАБОТКА ПРОГРАММЫ ДЛЯ ПРОГНОЗИРОВАНИЯ ЕМКОСТИ РЫНКА ТОВАРОВ И УСЛУГ

Объектом исследования является емкость рынка закупаемых государством товаров (услуг). Используя информационные технологий создана модель, которая прогнозирует емкость рынка товаров и услуг, реализованная в виде программы. В данной программе используются открытые данные о государственных закупках, на основе которых составляется прогноз объемов закупок.

Объем закупок, равно как и цена на них, представляют собой последовательность данных для построения прогноза которой используется анализ имеющихся временных рядов.

Образец таблицы с данными приведен в Таблице 1. При этом используются данные только по определенному наименованию товара (услуги).

Таблица 1.

Пример таблицы с данными

При написании программы моделирования необходимо учитывать общие логические правила, определяющие поведение системы. В общем виде при исследовании временного ряда  выделяются несколько составляющих (аддитивная модель):

 = T + S +C + E, 

где (t = 1, 2,…, n),

или мультипликативная модель:

 = T * S *·C * E,

здесь T – тренд, плавно меняющаяся компонента, описывающая чистое влияние долговременных факторов, т. е. длительную («вековую») тенденцию изменения признака (например, рост цен, увеличение / уменьшение количества закупаемых товаров, объемы бюджетов различных регионов и т. п.);

Согласно Рисунку 1 можно видеть, как отличаются объемы финансирования в различных субъектах Российской Федерации исходя из заключенных контрактов.

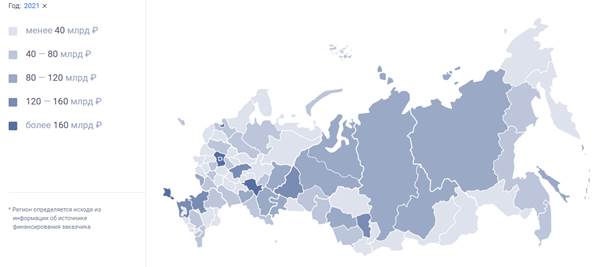
Рисунок 1. Распределение общей суммы размещенных контрактов в разрезе субъектов Российской Федерации

S – сезонная компонента, отражающая повторяемость экономических процессов в течение не очень длительного периода (года, иногда месяца, недели и т. д., например, начало и конец года, когда многие заказчики осуществляют основное количество закупок). На рисунке 2 изображен примерный график заключения государственных контрактов в течение одного календарного года;

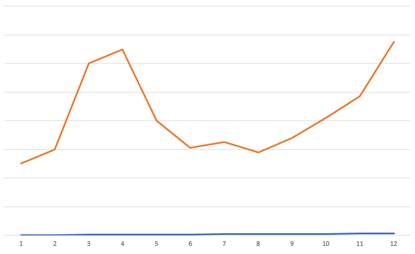
Рисунок 2. График заключения государственных контрактов

C – циклическая компонента, отражающая повторяемость экономических процессов в течение длительных периодов (например, влияние волн экономической активности Кондратьева, демографических «ям», циклов солнечной активности и т. п.);

E – случайная компонента, отражающая влияние не поддающихся учету и регистрации случайных факторов.

Следует обратить внимание на то, что в отличие от E, первые три составляющие (компоненты) T, S, C являются закономерными, неслучайными. Важнейшей классической задачей при исследовании временных рядов является выявление и статистическая оценка основной тенденции изменений объемов и цен закупаемых товаров.

К основным этапам анализа временных рядов можно отнести:

• графическое представление и описание поведения временного ряда;

• выделение и удаление закономерных (неслучайных) составляющих временного ряда (тренда, сезонных и циклических составляющих);

• сглаживание и фильтрация (удаление низко- или высокочастотных составляющих временного ряда);

• исследование случайной составляющей временного ряда, построение и проверка корректности выбранной математической модели;

• прогнозирование развития изучаемого процесса на основе имеющегося временного ряда;

• исследование взаимосвязи между различными временными рядами.

Среди наиболее распространенных методов анализа временных рядов можно выделить корреляционный и спектральный анализ, модели авторегрессии и скользящей средней.

Если выборка , ,, ..., , …, , рассматривается как одна из реализаций случайной величины X, временной ряд , ,, ..., , …, , рассматривается как одна из реализаций (траекторий) случайного процесса X(t). Вместе с тем следует иметь в виду принципиальные отличия временного ряда , (t = 1, 2, ..., n) от последовательности наблюдений , ,, ..., , …, , образующих случайную выборку. Во-первых, в отличие от элементов случайной выборки члены временного ряда, как правило, не являются статистически независимыми. Во-вторых, члены временного ряда не являются одинаково распределенными.

На сегодняшний день методы анализа и прогнозирования временных рядов далеки от совершенства — они все еще основаны на традиционных статистических принципах и простых алгоритмах машинного обучения, таких как ансамбли деревьев и линейная аппроксимация. Но при этом позволяют с определенной точностью построить прогнозную модель и использовать ее в программном продукте.

В данной статье были рассмотрены основные модели исследования временных рядов, основные этапы их анализа, которые используются в процессе создания программного обеспечения, которое позволяет пользователю достоверно составить финансовый план, рассчитать расходы на закупку сырья, его хранение, возможные объемы производства в зависимости от сезона, грамотно распределить имеющиеся ресурсы, снизить издержки и увеличить прибыль предприятия.