МЕТОДИКА РАЗДЕЛЕНИЯ СИСТЕМАТИЧЕСКОЙ И СЛУЧАЙНОЙ НЕСИММЕТРИИ НАПРЯЖЕНИЙ И ТОКОВ

При анализе несимметрии необходимо учитывать не только модули, но и фазы исходных напряжений и их симметричных составляющих, расчет которых при известных значениях модулей и фазовых сдвигов напряжений на любом отдельно взятом интервале измерений не представляет сложностей. Система координат при этом выбирается таким образом, чтобы вещественная ось была совмещена с вектором одного из напряжений (обычно фазы «А»), а вещественные и мнимые части симметричных составляющих определяются проекциями на оси  векторов напряжений (векторы фаз «В» и «С» при этом поворачиваются на угол + 120^о и – 120^о соответственно). Согласно методу симметричных составляющих напряжение прямой последовательности фазы «А» равно:

;           (1)

В пределах определенного интервала составляющие обратной и нулевой последовательностей относительно той же оси составляют:

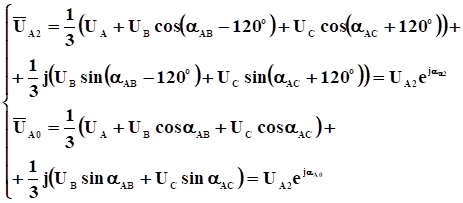.         (2)

Угол фазового сдвига напряжения прямой последовательности  от вектора  весьма мал, поэтому его удобнее всего определять, по отношению мнимой и вещественной составляющих:

.                                        (3)

Геометрическая интерпретация уравнения (3) дана рисунке 1.

Рисунок 1. Определение вектора напряжения прямой последовательности  относительно оси фазы «А»

В процессе изменения напряжений напряжение  изменяется не только по величине, но и по фазе, поэтому данная система координат не остается неподвижной, и симметричные составляющие на различных интервалах определяются относительно различных осей. Это исключает возможность арифметического суммирования их проекций, определения среднего значения и вероятностных характеристик на всем периоде измерений, что является существенным недостатком.

Рассмотрим теперь ту же самую несимметричную систему напряжений, но относительно системы координат, вещественная ось которой совмещена с вектором напряжения прямой последовательности. Для этого необходимо умножить все напряжения на единичный оператор поворота , что равносильно их повороту на угол α₁ в противоположном направлении. При этом для напряжения прямой последовательности и полного напряжения фазы «А» имеем:

 ,

а для повернутых на ± 120^о векторов напряжений фаз «В» и «С»:

 .

Теперь для симметричных составляющих фазы «А», выраженных через их проекции на оси Re’ и Im’, получаем:

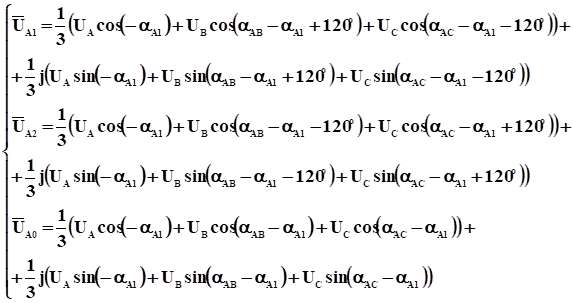 (4)

В новой системе координат все симметричные составляющие выражаются относительно одной оси, которую можно для них считать неподвижной, поэтому при случайном изменении напряжений можно определить средние значения их ортогональных проекций, а также модуль и фазу полных напряжений:

;   .                         (5)

;  .                      (6)

На любом i-том интервале активная и реактивная составляющие любого напряжения равны сумме их средних значений  и случайных приращений :

;    ,               (7)

причем суммы этих приращений тождественно равны нулю:

; .

Таким образом, на каждом интервале вектор полного напряжения определяется геометрической суммой вектора среднего значения и вектора приращения: , а геометрическая сумма этих векторов равна вектору среднего значения напряжения: . По средним значениям ортогональных составляющих фазных напряжений всегда можно определить ортогональные проекции соответствующих им симметричных составляющих, которые и характеризуют систематическую несимметрию. Вектор  остается неизменным как величине, так и по фазе на любом интервале. Случайные составляющие на различных интервалах имеют по отношению к систематической составляющей различные аргументы. Их модули находятся в пределах:

,

и на отдельных интервалах могут как меньше, так и больше модулей напряжения .

Для наглядности на рисунке 2 показана геометрическая интерпретация первого уравнения системы (4) в преобразованной системе координат.

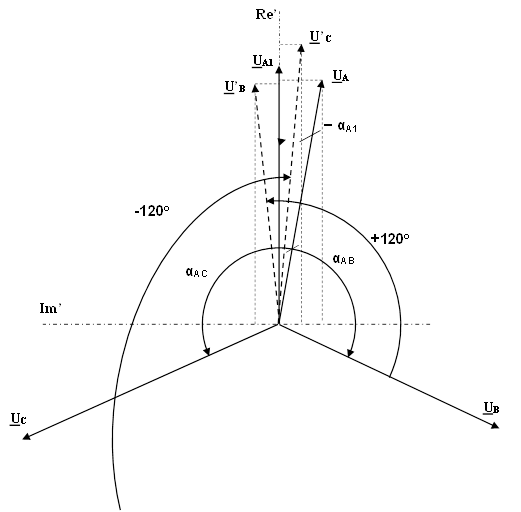
Рисунок 2. Определение проекций напряжений относительно оси напряжения прямой последовательности фазы «А»

Уравнения ортогональных проекций напряжений обратной и нулевой последовательности интерпретируются аналогично, но с учетом того, что для обратной последовательности векторы фаз «В» и «С» поворачиваются на 120^о в противоположных направлениях, а для нулевой последовательности не изменяются.

ГОСТ 13109–97 регламентирует только модули коэффициентов несимметрии, которые определяются отношениями составляющих обратной и нулевой последовательности к напряжению прямой последовательности: ; , поэтому даже в случае полной компенсации систематической несимметрии случайная составляющая может оказаться недопустимо большой.

На рисунке 3 показаны суточные диаграммы изменения модулей полного коэффициента несимметрии напряжений по нулевой последовательности и его случайной составляющей, определенные по изложенной методике с использованием данных, полученных при регистрации ПКЭ на шинах ТП.

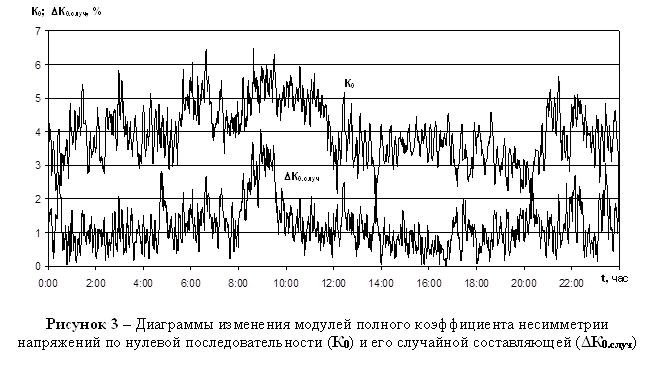
Расчет по методу преобразования координат дал следующие результаты: среднее значение модулей полного коэффициента несимметрии составляет 3,99%, модуль и аргумент систематической составляющей: ; . Значение модуля систематической составляющей близко к среднему значению модулей полного коэффициента, что свидетельствует о большой доле систематической несимметрии.

Чтобы установить соответствие показателей несимметрии требованиям ГОСТ 13109 – 97 при исключенной систематической составляющей, рассмотрим диаграмму изменения случайной составляющей.

Среднее значение модулей для нее значительно уменьшилось, и составляет: .

Однако при стандартном отклонении  верхняя граница интервала, в который попадают 95% значений  составляет 2,54%, что выше нормально допустимого значения, и даже полное устранение систематической несимметрии в данном случае не выполнения норм ГОСТ 13109-97.

Практическое значение данного метода заключается в возможности обоснованного выбора наиболее эффективных мероприятий по снижению несимметрии напряжений.