DEVELOPMENT OF AN APPLICATION FOR GRAPHICAL ANALYSIS OF FUNCTIONS BY MEANS OF THE JAVA PROGRAMMING LANGUAGE

Anastasia Dyatlova

Student of the Russian University of Transport (MIIT), Russia, Moscow

Аннотация. В статье разработана концепция приложения, реализованы и отлажены данные приложения средствами кроссплатформенного языка программирования JAVA. Разобраны и модифицированы для приложения многие классические алгоритмы.

Abstract. The article develops the concept of the application, implements and debugs these applications using the cross-platform JAVA programming language. Many classical algorithms have been disassembled and modified for the application.

Ключевые слова: математический анализ, исследование функций, приложение, JAVA;

Keywords: mathematical analysis, function research, application, JAVA;

Введение

Компьютеры являются основными средствами хранения и обработки информации, сегодня их вычислительные возможности используют для решения многих математических задач. Задача об исследование функции и применение для ее решения различных вычислительных методов очень универсальна, подобные задачи  существуют в экономике, логистике, технике и других областях.

Так что создание собственного приложения для обработки и исследования функции предшествует таким дисциплинам как: «Математические модели в экономике», «Защита информации», «Корпоративные информационные системы», «Методы оптимизации» ООП.

Исследование функции является важной частью математического анализа, ускорение данного процесса путем создания алгоритмов для решения данной задачи и их реализация на языке программирования может использоваться для развития этой области математического анализа.

В процессе создания приложения для исследования математических функций мне пришлось овладеть множеством новых для меня возможностей языка программирования JAVA, а также изучить множество математических методов, таких как метод бисекции, метод хорд и касательных, а также алгоритмов вычисления производных в точке и алгоритм перевода выражения в Обратную польскую запись и обратно.

Также данное приложение можно развивать в дальнейшем, так как данная область математического анализа обширна и существует множество других методов для исследования функции.

Концепция приложения

Созданное мною приложение позволяет исследовать математические функции, а именно строить график функции, находить нули, экстремумы,  производные первого и второго порядка в точке.

Приложение состоит из 2 частей: графической, используемой для работы с графиком функции, и части, содержащей интерфейс программы. Входными данными программы является функция заданная аналитически и участок, на котором она будет исследоваться, при некорректно введенных данных выводится сообщение об ошибке. После того как правильно введены исходные данные необходимо нажать на кнопку “Исследовать функцию”, после чего программа выведет график функции, ее нули и экстремумы. Также приложения позволяет при наведении мыши на график функции узнавать x и y координату этой точки и строить касательную к функции в этой точке, при этом выводя значения производной 1-ого и 2-ого порядка. Такой же результат можно получить, если ввести в соответствующем поле  значение аргумента, в которой надо вычислить производные и построить касательную.

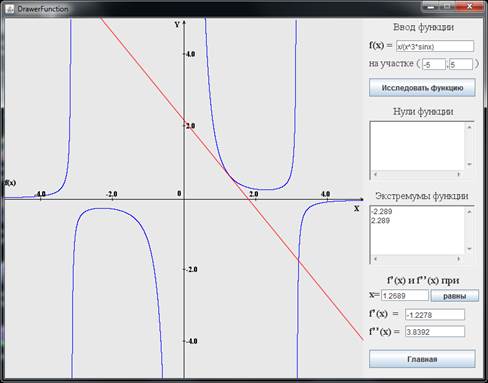
Рисунок 1. Скриншот приложения.

Получения значения функции заданной строкой

В данной программе функция задается пользователем аналитически в соответствующем поле, т.е программа получает входные данные типа String. Для получения значений функции в приложении используется алгоритм обратной польской записи. Данный алгоритм является классическим решением данной задачи.

Постановка задачи

На вход программы поступает выражение, состоящее из односимвольных идентификаторов и знаков арифметических действий. Требуется преобразовать это выражение в обратную польскую запись или же сообщить об ошибке.

Алгоритм перевода в обратную польскую запись

На вход программы поступает выражение, состоящее из односимвольных идентификаторов и знаков арифметических действий. Требуется преобразовать это выражение в обратную польскую запись или же сообщить об ошибке. В программе используется 2 стека типа String. Необходимо использовать приоритеты математических операций.

Таблица 1.

Приоритеты операций

1) В стек (стек – это структура данных, хранящая совокупность однотипных элементов, которые поступают в стек и выходят из него по правилу «последний вошел - первый вышел») будут помещаться только символы операций.

2) Символы операндов из входной строки поступают сразу в выходную строку.

3) Символы операций сначала поступают в стек и при определенных условиях выталкиваются в выходную строку.

4) Открывающаяся скобка всегда попадает в стек.

5) Закрывающаяся скобка ни в стек, ни в выходную строку не попадает.

6) Когда встречается в выходной строке закрывающаяся скобка, из стека выталкиваются все символы до первой встречной открывающейся скобки включительно. Причем знаки операций выталкиваются в выходную строку, а открывающаяся скобка пропадает.

7) Если во входной строке текущий символ – знак операции, то сравниваются приоритеты операций из строки и верхушки стека.

8) Если приоритет операции из входной строки больше приоритета операции из верхушки стека, то операция из входной строки стека перемещается в стек. В противном случае из стека выталкиваются все операции с приоритетами большими либо равными приоритетам операций из входной строки. После чего операция из входной строки помещается в стек.

9) При встрече конца входной строки содержимое стека выталкивается в выходную строку.

Построение графика функции

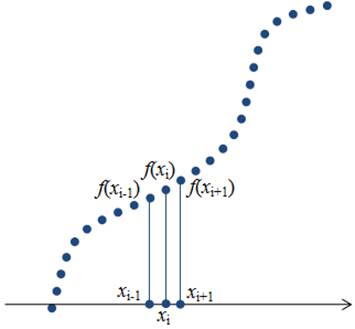
Рисунок 2. Дискретная функция

После того как задано аналитическое выражения функции программа строит ее график дискретной функции (рисунок 2) в декартовой системе координат на заданном участке от A до B. Для этого на этом участке программа находит 20000 (число подбиралось из вычислительных возможностей компьютеров) значений на этом участке и соединяет их прямыми, проверяя при этом на наличие  вертикальные асимптоты. Также для графического отображение отображения функции необходимо определить размерность, т.е нужно узнать сколько будет занимать единичный отрезок в пикселях. Для этого я использую переменную  SIZE равную отношению ширины графика в пикселях к ширине заданного отрезка в координатах.  Чтобы получить координаты точек в пикселях необходимо умножить их значения на переменную SIZE.

SIZE=WIDTH/(B-A);//  где WIDTH ширина окна графика в пикселях

Все значения функции после вычисления помещаются в двумерный массив размерностью [20000][3]. Где [i][0] – значение x, [i][1] – значение f(x), а [i][2] флаг определяющий будет ли рисоваться прямая между данной точкой и следующей.

Алгоритм:

1)В цикле перебираем значения x на участке от A до B с заданным интервалом и вычисляем для каждого x значения функции.

2) Для каждого x проверяем, чтобы f(x) или f(x+интервал) лежит на участке ((B-A)/2;(A-B)/2), если выполняется, то кладем x и f(x) в соответствующие ячейки двумерного массива.

3) Если выполняется предыдущее условие то накладываем еще одно условие: если f(x1) <= f((x1+x2)/2) <= f(x2) и |f(x1)-f(x2)|<(b-a) то элемент массива [i][2] (флаг) = 1 (правда).

3)При начальной отрисовке и дальнейшей перерисовке отрезок строится по двум соседним точкам, при выполнении условия |f(x1)-f(x2)|<=B-A.

Вычисление производной 1-ого и 2-ого порядка в точке

В приложении для вычисления первой и второй производной используется трехточечный метод для поиска производных. Для  двухточечных методов при вычислении производных используется значение функции в двух точках, для трехточечных методов значение в трех точках. На рисунке 3 представлена иллюстрация трехточечного метода, который используется в моем приложении, численное значение тангенса угла α, образованного касательной к графику y(x) и осью абсцисс, показывает точное значение производной (геометрический смысл производной). Тангенс угла α₃ наиболее приближен к значению производной в этой точке, этим и обусловлен выбор данного метода для нахождения производной. 

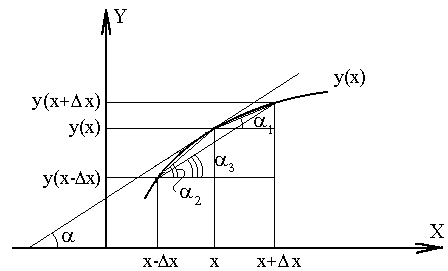
Рисунок 3. Графическое представление вычисления нахождения функции

В программе вычисление производной первого порядка происходит по формуле:

f′(x)=(f(x+Δx)-f(x-Δx))/(2*Δx)

Используя значение производной первого порядка в точке, программа строи касательную в этой точке, используя математическую формулу

y= f(x0)+ f′(x0)(x-x0)

Что касается вычисления производной второго порядка в точке, то она вычисляется как первая производная от функции  y=f′(x), т.е. вместо значений y(x), y(x+ Δx), y(x- Δx) используются значения  y′ (x), y′ (x+ Δx) и y′ (x- Δx).

Поиск нулей на участке. Метод бисекции. Метод хорд и касательных

Для поиска нулей функции на заданном участке я использую 2 метода поиска нулей: это метод бисекции и метод хорд и касательных. Данные методы используются только для участка функции, на котором существует 1 ноль,  так что в программе выделяется область с нулем, а затем запускается один из методов.

Метод бисекции.

Метод бисекции или метод деления отрезка пополам — простейший численный метод для решения нелинейных уравнений вида F(x)=0. Предполагается только непрерывность функции F(x). Задача заключается в нахождении корней нелинейного уравнения F(x)=0  (Рис 3.) Возьмем отрезок разбиения [a,b], такой, что f(a)<0<f(b) (или f(b)<0<f(a)). До тех пор пока длина отрезка [a,b]>2eps будем выполнять циклично следующие операции:

• найдем среднюю точку отрезка [a,b] c = (a+b)/2.
• Если f(c)=0, то корень найден, КОНЕЦ.
• Если f(a)*f(c)<0, тогда b=c, иначе a=c.

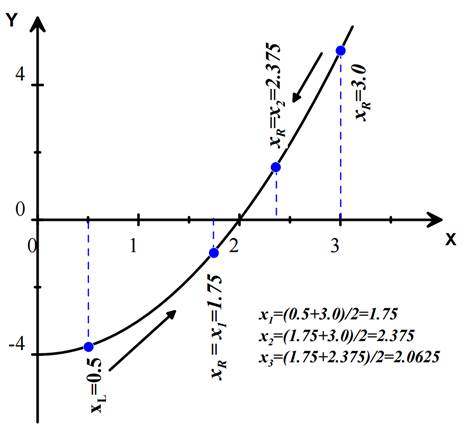
Рисунок 4. Графическое представление метода бисекции (деления отрезка пополам)

Метод хорд и касательных.

Суть комбинированного метода состоит в разбиении отрезка [a,b]  на три отрезка с помощью хорды и касательной, и выборе нового отрезка от точки пересечения хорды с осью абсцисс до точки пересечения касательной с осью абсцисс, на котором функция меняет знак и содержит решение. Построение хорд и касательных продолжается до достижения необходимой точности решения ε=0.000001.

Комбинированный метод применим для решения уравнения вида f(x)=0 на отрезке [a,b], если ни одна точка отрезка [a,b] не является ни стационарной, ни критической, т.е. f’(x)≠0 и f”(x)≠0.

Сначала находим отрезок [a,b] такой, что функция f(x) дважды непрерывно дифференцируема и меняет знак на отрезке, т.е. f(a)f(b)<0.

Далее применяем алгоритм решения.

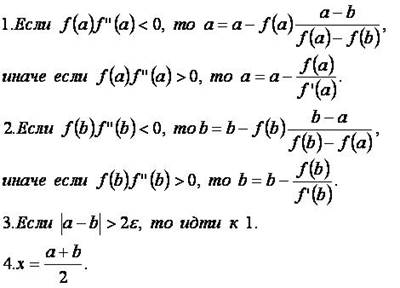
Условия запуска алгоритмов поиска нулей (отделение участков функции с 1 нулем).

При запуске построения графика заданной функции, для каждого полученного значения проверяется 2 условия. При выполнении первого запускается метод бисекции, а при выполнении 2 запускается метод хорд и касательных, где (a,b) это участок, на котором исследуется функция. Для ускорения выполнения программы вычисляются первые 1000 нулей функции на заданном участке каждый в отдельном потоке.

Условие запуска алгоритма поиска нулей функции.

1) Если функция меняет свой знак 1000, то запускается метод бисекции.

2) Иначе если функция больше нуля (во всех проверяемых значениях) убывает затем возрастает и в точке приближенной к экстремуму функция имеет значение близкое к нулю или если функция меньше нуля (во всех проверяемых значениях) функция возрастает, затем убывает и в точке приближенной к экстремуму функция имеет значение близкое к нулю, то запустить метод хорд и касательных.

Поиск экстремумов функции на участке

Для поиска экстремумов функции в приложении используется метод итерации, он происходит во время вычисления значений функции.

Если до определенного значения x функция убывает, затем она возрастет и наоборот (возрастала, а затем убывала) то точка x это приближенное значение экстремума функции.

Данный алгоритм не является лучшим решением, но остальные способы решения этой задачи не рассчитаны на любую функцию. В дальнейшем я бы хотел реализовать поиск экстремумов с помощью нахождения функции производной путем усовершенствования алгоритма обратной польской записи. Нули функции производной являются экстремумами функции.