ПРИМЕНЕНИЕ РЕГРЕССИОННОГО АНАЛИЗА ДЛЯ ВЫЯВЛЕНИЯ ФАКТОРОВ, ВЛИЯЮЩИХ НА ЧИСЛЕННОСТЬ НАСЕЛЕНИЯ

Аннотация. Статистика населения – демографическая статистика, или просто демография, - один из важнейших разделов социально-демографической статистики. В статье рассматривается применение регрессионного анализа для выявления влияния социально-экономических показателей на численность населения.

Ключевые слова: регрессионный анализ, численность населения.

Одной из важных потребностей в управлении социально-экономическими процессами является изучение численности и состава населения, так как с одной стороны население выступает в качестве производителя национального богатства, а с другой стороны — является потребителей духовных и материальных ценностей. Широк круг проблем, прямо или косвенно связанных с населением. Исходя из этого — существует много факторов, напрямую влияющие на численность населения, которые рассмотрены в данной статье.

Цель данной работы - провести анализ по всем субъектам, в которых определяются важные показатели численности населения. Такой анализ позволит субъектам выделить слабые места, в которые стоит вкладывать средства для повышения численности населения.

Для проведения анализа выбрано 76 регионов РФ. Выявлен ряд важных показателей, которые влияют на численность населения.

В анализе зависимой переменной является y - численность населения, тыс. чел., а независимыми переменными являются: Х1 – Коэффициент родившихся (чел. на 1000 человек населения), Х2 – Коэффициент умерших (чел. на 1000 человек населения), Х3 – Естественный прирост/yбыль (чел.), Х4 – Продолжительность жизни (лет), Х5 – Количество заключенных браков (чел. на 1000 человек населения) Х6 – Количество разводов (чел. на 1000 человек населения) Х7 – Коэффициент миграционного прироста (чел. на 1000 человек населения), Х8 – Величина прожиточного минимума (рyб.), Х9 – Среднемесячная заработная плата работников(руб.), Х10 – Удельный вес автомобильных дорог с твердым покрытием (общая протяженность), Х11 – Ввод в эксплуатацию жилых домов (тыс. м2), Х12 – Число зарегистрированных преступлений (ед. на 100 000 чел. населения), Х13 – Численность безработных (тыс. чел),      Х14 – Индексы  потребительских цен (%), Х15 – Число дошкольных учреждений (ед.), Х16 – Число образовательных учреждений, реализующих программы среднего профессионального образования (ед.  ), Х17 – Число образовательных учреждений, реализующих программы высшего профессионального образования (ед.), Х18 – Численность населения на одну больничную койку (на конец года; человек).

В связи с небольшим количеством наблюдений – 76, для проведения анализа использовался метод моделирования измеряемых данных и исследования их свойств.

Регрессионный анализ, пожалуй, является наиболее широко используемым статистическим методом для исследования или оценки взаимосвязи между зависимыми и набором независимых объясняющих переменных. Он также используется в качестве общего термина для обозначения различных методов анализа данных, которые используются в качественном методе исследования для моделирования и анализа многочисленных переменных. В методе регрессии зависимая переменная является предиктором или объясняющим элементом, а зависимая переменная - результатом или ответом на конкретный запрос. Суть регрессионного анализа заключается в нахождении наиболее важных факторов, которые влияют на зависимую переменную.

Построив и проанализировав матрицу парных коэффициентов корреляции были выявлены что «Ввод в эксплуатацию жилых домов» (X₁₁) имеют коэффициент корреляции равный 0,87, «Численность безработных» (X₁₃) имеет коэффициент 0,83, «Число дошкольных учреждений» (Х₁₅) имеют коэффициент 0,91, «Число образовательных учреждений, реализующих программы среднего профессионального образования» (Х₁₆) имеют коэффициент 0,89, «Число образовательных учреждений, реализующих программы высшего профессионального образования» (Х₁₇) имеют коэффициент 0,87. Вышеописанные факторы влияют на «Число населения» больше чем все остальные.

Следующим шагом будет сравнение процедуры «пошагово с включением» и «пошагово с исключением», а также сравнение с данными процедурами после стандартизации значений. После сравнения полученных результатов было решено использовать итоги регрессии с использованием процедур «Пошаговая с включением», так как в данной модели стандартная ошибка меньше чем во всех остальных, а R2 больше.

Построим уравнение регрессии:

Y = 0,19Х₁₅ + 0,37Х₁₁ + 0,29Х₁₃ + 0,14Х₁₆ + 0,14Х₁₇ - 0,09Х₁ - 0,02Х₁₄

F (7,74) = 667,91

F_кр (0,05;7,74) = 2,02

R₂ = 0,98 – Коэффициент линейной детерминации показывающий зависимость одной переменной от других.

скор. R₂ = 0,98

Стандартная ошибка оценки (S) = 166,76

Статистика Дарбина-Уотсона (Dw) = 1,84

Нормальность распределения переменной оценивается по полученным остаткам. Для этого построен нормальный вероятностный график остатков (Рисунок 1) и распределение остатков (ожидаемое нормальное) (Рисунок 2).

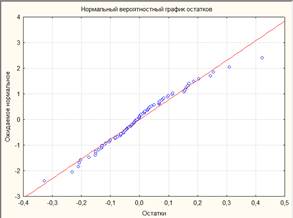
Рисунок 1. Нормальный вероятностный график остатков

Рисунок 2. Распределение остатков

По графикам видно, что остатки образуют прямую зависимость и подчиняются нормальному закону распределения.

Так как R2 больше 0,7, то это говорит нам о средней точности аппроксимации, то есть модель хорошо описывает явление. Уравнение значимо так как F > Fкр и гипотеза об отсутствии линейной связи отклоняется.

В результате регрессионного анализа выяснилось:

Если «Число дошкольных учреждений» (Х₁₅) увеличить на 1 единицу, то «Численность населения» увеличится на 1 тыс. человек при прочих неизменных факторах.

Если «Ввод в эксплуатацию жилых домов» (Х₁₁) увеличить на 1 тыс. кв. метров, то «Численность населения» увеличится на 0,37 тыс. человек при прочих неизменных факторах.

Если «Число образовательных учреждений, реализующих программы среднего профессионального образования» (Х₁₆) увеличить на 1 единицу, то «Численность населения» увеличится на 7,55 тыс. человек при прочих неизменных факторах.

Если «Число образовательных учреждений, реализующих программы высшего профессионального образования» (Х₁₇) увеличить на 1 единицу, то «Численность населения» увеличится на 22,67 тыс. человек при прочих неизменных факторах.