РАСЧЕТ ОСТАТОЧНОГО РЕСУРСА ПО КОРРОЗИОННОМУ РАСТРЕСКИВАНИЮ МЕТАЛЛИЧЕСКИХ ТРУБОПРОВОДОВ

Аннотация. В статье рассмотрены пути решения проблемы, связанные с коррозийным растрескиванием. Реализован конкретный пример расчета по описанному алгоритму.

Ключевые слова: общая коррозия, трубопроводы гидроэнергетики, коррозионное растрескивание.

Введение. Высокая агрессивность сред, вызывающая коррозию внутренних технологических поверхностей энергетического оборудования, ежегодно приводит к значительному экономическому и экологическому ущербу.

Трубопроводы гидроэнергетики подвержены коррозионному износу, в результате чего срок их службы значительно сокращается. Проблема коррозии особенно актуальна в энергетике. Трубопроводы изготавливаются из низколегированной углеродистой стали. Теплоносителем является не просто чистая вода, а вода с растворенной в ней газами, которая способствует значительной коррозии металла в трубопроводах.

Следует подчеркнуть, что становится важным влияние напряженно-деформированного состояния на скорость коррозионно-эрозионного изнашивания. Например, деформация 1 % увеличивает скорость коррозии кремнистого железа в 0,01 % растворе серной кислоты на 53 % по сравнению с недеформированным металлом.

Основная часть. В настоящей работе представлен аналитический подход к определению ресурса элементов конструкций трубопроводов на основе теории металлических оболочек с учетом напряженно-деформированного состояния и коррозионного износа элементов.

Ранее изучалось коррозионное растрескивание металлов под напряжением. Это явление имеет место при определенных критических значениях растяжения, определяемых действующими напряжениями и потенциальной энергией. Напряжения меньше критических влияют на общую коррозию, вызывая растрескивания [3].

Одной из первых работ в этом направлении была статья Корнишина [2], в которой рассматривается совместное решение уравнения коррозии, представляющего собой линейную зависимость скорости коррозии от напряжения, и уравнений, описывающих напряженно-деформированное состояние оболочки переменной толщины. Далее система совместных уравнений, описывающая поведение оболочки в агрессивной среде, решается в конечных разностях по двухслойной явной схеме с шагом по времени.

В работе автор [2], рассматривает совместное решение уравнения коррозии, представляющего собой линейную зависимость скорости коррозии от напряжения, и уравнений, описывающих напряженно-деформированное состояние оболочки переменной толщины. Далее рассматривается система совместных уравнений, описывающая поведение оболочки в агрессивной среде, решается в конечных разностях по двухслойной явной схеме с шагом по времени.

На сегодняшний день существует ряд полуэмпирических моделей, аппроксимирующих коррозионный износ с учетом напряженного состояния.

Металлические конструкции широко применяются в современной технике, в частности, при изготовлении металлических элементов в энергетике. Это, в первую очередь трубопроводы, отводы и др. Эти элементы отличаются высокой прочностью, жаростойкостью, коррозионной стойкостью.

Рассмотрим цилиндрическую металлическую оболочку при воздействии агрессивной среды [4]. Такие задачи очень важны при проектировании трубопроводов электростанций (коррозионное растрескивание).

Скорость изменения толщины в данной точке оболочки принимается в виде:

                                                                                       (1)

с начальным условием:

                                                                                                (2)

где х, у — нормальные координаты срединной поверхности оболочки;

 Т - температура;

 σ — функция, связывающая скорость изменения толщины оболочки с напряжённым состоянием в точке поверхности.

Обратите внимание, что F — известная функция, форма которой определяется из эксперимента, а  — конечный момент времени.

Мы изучаем влияние напряженного состояния на общую коррозию в предположении, что скорость коррозии является линейной функцией интенсивности напряжения.

Уравнения коррозионного износа записываются следующим образом:

                                                                                 (3)

Здесь  — интенсивность напряжений на поверхности биметаллической оболочки;

α и k — конечные коэффициенты;

φ(t)— безразмерная функция времени.

Как правило, в большинстве практических случаев φ(t) является постоянной или монотонно убывающей функцией. К уравнению необходимо добавить уравнения теории металлических оболочек. (1) или (3).

В результате получаем несвязанную задачу теории оболочек, с учетом которой к решению уравнения (1) можно применить конечно-разностную аппроксимацию по времени (3).

Таким образом, алгоритм решения начально-краевой задачи сводится к совместному решению уравнения (3) при начальных условиях в уравнении (2) и система уравнений для биметаллических оболочек в общем случае переменной толщины при соответствующих граничных условиях. Более того, на каждом временном шаге из уравнения (3) получаем численные значения толщины элемента конструкции, которые затем используются для построения сплайн-функций [1]. Затем решается система уравнений биметаллических оболочек, из решения которой определяются значения .

Критерием прекращения пошагового процесса является условие:

где  – предел текучести материала элемента конструкции.

Ресурс элементов конструкции атомных энергоблоков в целом определяется суммированием шагов по времени.

Получим уравнение равновесия металлической оболочки на основе вариационного принципа Лагранжа:

                                                                                                   (4)

Здесь  — изменение потенциальной энергии деформации оболочки;

  — вариация потенциала внешних сил, равная вариации работы внешних сил, взятой с противоположным знаком. Запишем выражение для изменения потенциальной энергии:

                                                                           (5)

где  — потенциальная энергия деформации единицы поверхности оболочки. Интегрирование распространяется на всю поверхность перехода (рис. 1): от  =  до  =  и от  =  до = .

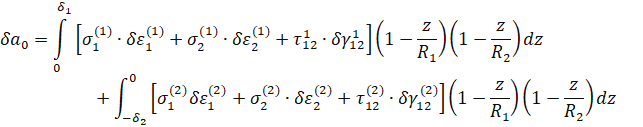
При анализе используются следующие допущения (рис. 1). Криволинейная система координат совпадает с линиями главных кривизн. Эта система координат является гауссовой системой координат, она ортогональна. Положение точки, не принадлежащей поверхности стыка, определяет координаты z-расстояния по нормали к точке от поверхности стыка (+, если она направлена по внутренней нормали к поверхности стыка).

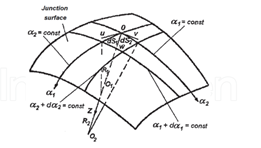
Рисунок 1. Система криволинейных координат на недеформированной поверхности стыка

Движения u и v являются направлением касательных к  и , а w — в направлении нормали к поверхности стыка. Деформации поверхности стыка определяются относительными удлинениями  и  в обоих направлениях  и , а также сдвигом изменением угла между касательными к прямым  и  (до деформации   , после  -  ).

Уравнение (5) можно представить следующим образом:

                                                     (6)

Обозначим через:

, ,  проекцию внешних поверхностных сил, отнесенных к единице поверхности стыка, на направление касательных к линиям кривизны  и  и нормали к поверхности стыка;

  ,   ,  ,  нормальные, поперечные, перерезывающие силы и изгибающий момент для сечения  = const;

  ,   ,  ,  то же для сечения  = const.

Тогда вариация потенциала внешних сил равна:

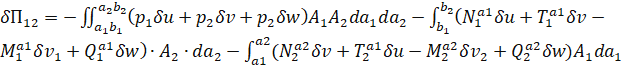                                          (7)

Подставляя уравнения. (6) и (7) в уравнении. (4) получаем:

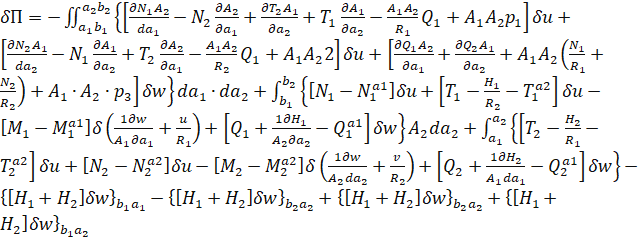                                        (8)

Здесь  и  — поперечные силы, возникающие в оболочке:

;                                                                                (9)

                                                                              (10)

Последние четыре члена в уравнении (8) есть работа сосредоточенных сил вдоль ребер оболочки  = const,  = const.

Заключение. Разработана теория коррозионного износа конструктивных элементов гидроэнергетики с учетом напряженного состояния и коррозионного износа.

Многочисленные факторы, влияющие на скорость процесса коррозионного изнашивания (степень агрессивности сред, температура, влажность и др.), учитываются в обобщенном виде путем составления дифференциального уравнения скорости изменения толщины элемента.

Разработан алгоритм решения задачи коррозионного износа металлических трубопроводов атомной энергетики с учетом напряженно-деформированного состояния элементов.