SUBSPACES OF VECTOR SPACES

Abstract. This article is designed to study various existing subspaces of linear spaces. The conclusions concluded in the practical part allow us to consider the ways of solving and applying them in practice and compare these subspaces with each other

Keywords: Vector space, subspace, linear space.

The set L of vectors of a linear space X is called a subspace if it follows from the fact that the vectors x, y belong to L that the vector ax + βy for any complex numbers α, β also belongs to the set L. [1]

1) Zero space {o}. In this case, V = {o}. Any field can be considered as F. The operations are defined in a trivial way: o+ o =o, αo=o. It is easy to verify that the specified set with such operations is a linear space over the field F." [2]

«2) Geometric spaces , , . The elements of this space are geometric vectors, i.e. directed segments, in space. A geometric vector whose beginning is at point A and the end is at point B is denoted by . Two vectors are considered equal if they are co-directed and have the same length. In view of this, it is convenient to assume that all vectors are fixed at one point O, called the pole or the origin. This consideration is also convenient because each vector is associated with a certain point of space — its end, and, conversely, a single vector is associated with each point of space, called the radius vector of the point, the beginning of which is fixed at the pole, and the end points to this point. Vectors are added according to the parallelogram rule: the sum of two radius vectors is the diagonal of a parallelogram built on these vectors. Vectors can be multiplied by real numbers. The product of the radius vector by the number α means a vector whose length is equal to the length of the original vector multiplied by |α|, and the direction coincides with the direction of the original vector if α > 0, and is replaced by the opposite if α < 0. Thus,  is a linear space over the field R. Analogous sets of vectors on a plane and on a straight line are denoted by ,  accordingly. These aggregates are also linear spaces over the field R.» [2]

«3) Arithmetic space . The elements of this space are columns of height n, composed of numbers. Two columns

, .

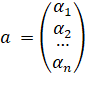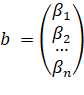we call them equal if . Numbers  и  are called components of vectors  and  accordingly.

The operations of adding columns and multiplying them by numbers from F are defined according to the following rules:

, 

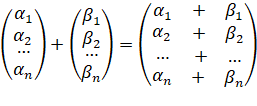It is also easy to check that  forms a linear space over the field F, called an arithmetic n-dimensional space. In particular, the zero vector in space  is .» [1]

«4) The space of polynomials F[x]. The elements of this space are polynomials with coefficients from the field F. It is easy to see that with respect to the usual operations of addition and multiplication of polynomials by numbers from F, the set V = F[x] forms a linear space over the field F. In particular, the zero vector in this space is the zero polynomial.» [2]

«5) Matrix space  . The elements of this space are matrices of given dimensions m × n with elements from the field A. It is easy to see that with respect to the operation of matrix addition and multiplication of matrices by numbers from A, the set  forms a linear space over the field F. In particular, the null vector in this space is the null m × n matrix.» [2]

We have considered some of the subspaces of linear space. Each of them is used in mathematics to achieve certain goals.

For example, take the vector space V, there is also a subspace: W2, W2.

Sometimes the intersection of two subspaces contains only the zero vector. If a set containing only a null vector were not considered a vector space, the statement in the first paragraph would be false. So one of the reasons why a vector space containing only a null vector is useful when answering questions about linear algebra is that it saves us from special cases that we have to pay special attention to. We would rather write "the intersection of W1 and W1 is a subspace" than write "the intersection of W2 and W2 is either a subspace or a set containing only a null vector".

Geometric spaces are also necessary, for example, in a metric space we can determine the distance between two points. Or the "event space", which plays an important role in the geometric interpretation of the theory of relativity. If it is necessary to work with numbers, then there is an arithmetic space for this. It defines the operations of addition and multiplication of numbers. It is advisable to work in the space of polynomials if the operations of addition and multiplication according to the conditions of the problem are defined over a set of polynomials, and if there is a need to perform actions with matrices, then we will use the matrix space.