GEOMECHANICAL JUSTIFICATION OF THE OPTIMAL PARAMETRS OF THE PIT SIDES BASED ON NUMERICAL MODELING

Abstract. In this study, the geomechanical justification of the optimal parameters of the sides of the “Dalnezapadny” quarry based on numerical modeling are investigated. We identify the factors affecting the stability of the instrument array of mining operations. The calculations of the stability of the sides of the quarry are carried out, then we used programs designed to assess the stability of cylindrical and non-cylindrical collapse surfaces in rocky and earthen slopes. Next, we present the results of geomechanical modeling by the limit equilibrium method in the table. In this work, we conduct research to determine the physical and mechanical properties of rocks and the stability of the sides of the «Dalnezapadny» quarry.

Aннотация. В данном исследовании исследуется геомеханическое обоснование оптимальных параметров бортов карьера “Дальнезападный” на основе численного моделирования. Мы выявляем факторы, влияющие на стабильность работы приборного комплекса при добыче полезных ископаемых. Проведены расчеты устойчивости бортов карьера, затем мы использовали программы, предназначенные для оценки устойчивости цилиндрических и нецилиндрических поверхностей обрушения на скалистых и земляных склонах. Далее мы представляем результаты геомеханического моделирования методом предельного равновесия в таблице. В данной работе мы проводим исследования по определению физико-механических свойств горных пород и устойчивости бортов карьера «Дальнезападный».

Keywords: quarry, optimal parameters, numerical modeling, "Slide" software.

Ключевые слова: карьер, оптимальные параметры, численное моделирование, программное обеспечение "Слайд".

To solve certain engineering problems of mining, in addition to a qualitative description of geomechanical processes, their quantitative assessment is necessary, which can be obtained because of field measurements of various manifestations of geomechanical processes or as a result of their modeling. Modeling has the advantage over full-scale measurements that it reveals the general qualitative and quantitative patterns of geomechanical processes. Mathematical modeling is often used to analyze geomechanical processes. [1, p.13] In engineering practice, various coefficients obtained empirically based on field observations or laboratory test data are used to account for factors that cannot be introduced into the calculation scheme. This approach is fraught with the effect of "accumulation of errors": the designer chooses the value of the coefficients he needs from a certain range, without having sufficient reason to choose these values. The more coefficients you need to enter, the more likely it is that the resulting value deviates from its true value and the greater this deviation. [4, p. 9] With the development of computer technology in mathematical modeling, numerical methods are increasingly used to solve various engineering problems of mining, along with traditional analytical methods.

A more accurate solution to the problem can be obtained if the design scheme and the solution method allow the factors of interest to the researcher to be taken into account initially. In this regard, the so-called numerical solution methods borrowed from the mechanics of a deformable solid open up wide possibilities. The most effective of them are the finite element method (hereinafter referred to as FEM) and the limit equilibrium method (hereinafter referred to as MPR). Their intensive development and application in the practice of engineering calculations became possible with the development and availability of computer technology. [2, p.21]

One of the methods of finite elements widely used in solving mining problems is the RS-2 program, and the "Slide" software developed by Rocscience is the method of ultimate equilibrium.

The stability analysis of the sides of the "Dalnezapadny" quarry was performed by the method of limiting equilibrium in the "Slide" software.

Stability calculation methods used in the “Slide” software package.

One of the types of calculating the stability of the sides of the quarry is the calculation of round-cylindrical sliding surfaces. [3, p. 5]

The calculation method is reduced to finding a design compartment with a minimum value of the ratio of horizontal projections of retaining and shear forces. The ratio of these values is taken as the calculated coefficient of stability margin. The calculation compartment means a part of the slope bounded from below by a given circular arc of sliding, and from above by the slope surface. Vertical lines into «columns» divide the calculation compartment less than one meter wide. The forces acting on the elementary column of the compartment are determined from the force triangle shown in Figure 1.

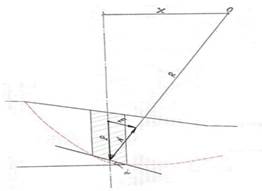
Figure 1. Forces acting on the elementary column of the calculation compartment

The stresses acting on the sliding surface are caused by the weight of the elementary rock compartment isolated within the prism of a possible collapse. The shear and normal forces acting on the prism of a possible collapse are determined by integrating elementary forces along the sliding surface. The holding forces are determined taking into account the strength characteristics of the rocks of the mountain range in accordance with the theory of ultimate equilibrium. [5, p. 16]

These programs are designed to assess the stability of cylindrical and non-cylindrical collapse surfaces in rocky and earthen slopes. The program analyzes the stability of sliding surfaces using the method of limiting equilibrium of vertical blocks, also known as the method of Janbu and Fellenius. For the analysis, a separate sliding surface can be taken, and a region of centers can be used to determine the location of critical surfaces for a certain area of the object under study. When performing calculations, the geometric parameters of the side of the quarry, as well as the rocks composing the instrument array, are entered into the programs. The programs use methods that satisfy the conditions of equilibrium of the collapse prism and its elements in the limiting state and take into account the stressed state of the array. [6, p. 19]

Slide software calculates the coefficient of stability margin and builds a critical sliding surface using the following methods: the Janbu method, the Morgenstern-Price method. All methods of limit equilibrium assume that the soil mass above the sliding surface is divided into. The sliding surface is considered to be of a round-cylindrical shape.

The Janbu method. The Janbu method is similar to Bishop's method. However, the Janbu method takes into account only the sum of the horizontal equilibrium forces, without taking into account the moment of equilibrium.

This method takes into account the forces between the blocks. As well as the equations of equilibrium forces in the horizontal and vertical directions for all blocks, the equation of the moment of equilibrium for all sections, except for the last, the highest. The reliability coefficient FS is determined by finding the direction of the forces acting between the blocks, and then the values of these forces are calculated. [7, p. 24]

The Morgenstern-Price method. This method also takes into account the forces between the blocks. The resultant shifting and holding forces that act between the blocks have different directions in each block (semi-sine function). The Morgenstern-Price method is more accurate in the sense that it takes into account all three equilibrium equations: the equations of equilibrium forces in the horizontal and vertical directions, as well as the equation of the moment of equilibrium. The reliability coefficient FS is determined by solving the equation of forces acting between the blocks and the reliability coefficient FS.

The Fellenius method. The usual block method (the Fellenius method) is applicable for inhomogeneous slopes and rock masses having adhesion and an angle of internal friction, where the sliding surface can be approximated by a circle. It is very convenient for complex calculations. Inaccurate for the analysis of the operating voltage with high pore pressure.

Calculation of the stability of the sides of the quarry based on the method of marginal equilibrium.

The initial analysis of the «Zhairem» deposit was carried out taking into account sensitivity. With this approach, a number of initial parameters were changed to construct a graph, which could then be used to understand the deviations in various parameters and their impact on the overall stability coefficient. [1, p.23 ]

When comparing the proportional ratios in the model with the properties of the array, only small deviations in strength, fracture intensity and morphology of violations are observed. This indicates that the Western and Far Western sections can be modeled as a homogeneous array within the framework of geomechanical analysis, without the need to separate them. [8, p. 26]

Slide software analyzes the stability of sliding surfaces using methods of extreme equilibrium with vertical or non-vertical slice. You can analyze individual sliding surfaces or apply search methods to determine the critical sliding surface for a given slope.

Next, Figure 2 shows the results of calculations performed by the method of limit equilibrium in Slide software.

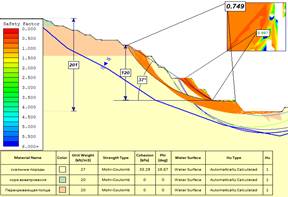
Figure 2. Results of numerical analysis by section

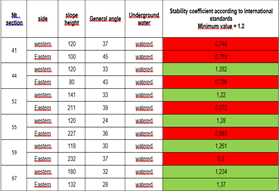
The results of geomechanical modeling by the limit equilibrium method are summarized in Table 1.

According to the results of numerical analysis, it can be seen that the instrument array of the eastern part of the quarry is in an unstable state (, whereas the western side of the quarry is generally stable. The eastern side of the Dalnezapadny quarry is designed with a steeper general angle than the western side, which led to the loss of stability of the instrument rock mass according to the results of numerical analysis by the finite element method.

Table 1.

Results of numerical analysis by the limit equilibrium method

Based on the analysis of the physical and mechanical properties of the rock mass, the results of previously performed geomechanical studies and the results of numerical analysis performed by the limit equilibrium method, a logarithmic dependence (Figure 9,16) of the change in the stability margin coefficient on the change in the general angle and height of the slope is constructed.

The logarithmic dependence is constructed by the method of least squares, based on minimizing the sum of the squares of the deviations of the selected function from the data under study.

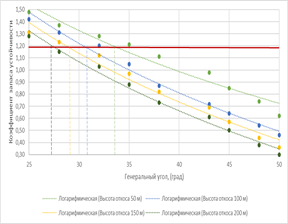
Figure 3. Graph of the dependence of the KZU on the general angle and height of the slope

Conclusion

1. Previously performed studies to determine the physical and mechanical properties of rocks and the stability of the sides of the Dalnezapadny quarry are analyzed in detail in order to obtain more reliable data on the structural features and strength properties of the instrument array.

2. On the basis of numerical simulation by the method of marginal equilibrium, the stability analysis of the sides of the "Dalnezapadny" quarry was performed. During the analysis, the program calculated the coefficients of the stability margin and constructed critical sliding surfaces (the collapse prism) using the Bishop method.

3. As a result of the analysis of the data obtained during computer modeling and the analytical method of least squares, a graph was constructed that allows determining the value of the stability margin coefficient depending on the change in the general angle and height of the slope.

Practical use of this investigation can be in the following branches of industry: mining, information technology.