ЛИНЕАРИЗАЦИЯ ОБРАТНОЙ СВЯЗЬЮ НЕЛИНЕЙНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ 2-ГО ПОРЯДКА В MATLAB SIMULINK

Рассматривается дифференциальное уравнение (далее ДУ)

где , известная функция, .[1-3]

Перейду к эквивалентной системе уравнений:

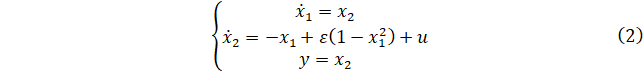
Выбрав управление, пользуясь приемом линеаризации обратной связи, запишу:

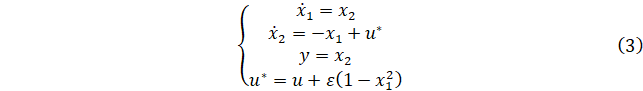
Построю в SIMULINK схемы, реализующие решения линеаризованного обратной связью исходного нелинейного ДУ и его линейный эквивалент. Схемы представлены на рисунке 1.

Рисунок 1. Схема в SIMULINK

Схема исходной нелинейной системы, используемой на рисунке 1, представлена на рисунке 2.

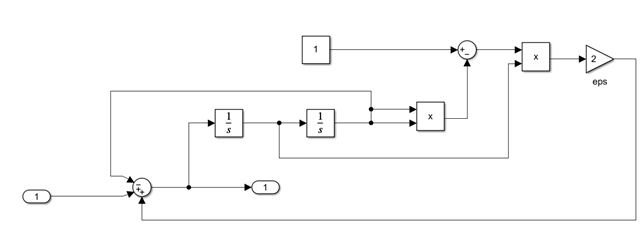
Рисунок 2. Схема нелинейной системы в SIMULINK

На рисунке 3 представлено решение линейной системы, системы линеаризованной обратной связью, а также разность этих решений.

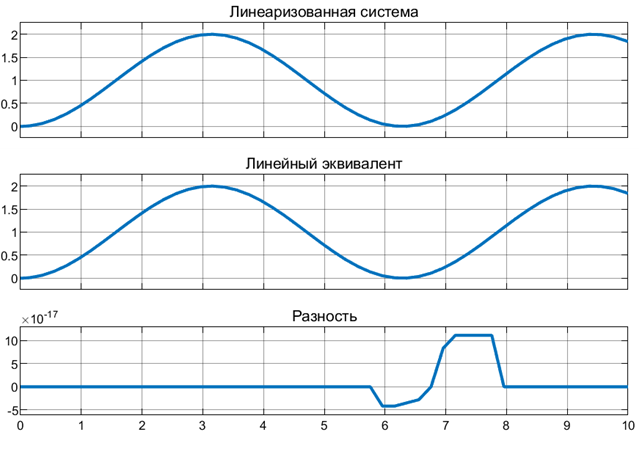
Рисунок 3. Решение в SIMULINK

Как следует из рисунка 3, решения для представленных систем тождественно совпадают.