Восстановление трёхмерной структуры по стереопаре

В последнее время широкое распространение приобрело такое направление кибернетики как компьютерное зрение, одним из основных аспектов которого является восстановление трёхмерной структуры объектов по набору фотографий или видео.

Существует множество алгоритмов восстановить трёхмерную сцену, но большая их часть требует некоторых дополнительных сведений, например параметры камеры, или расстояние между положениями камеры между снимками (как правило, речь идёт о двух камерах, расположенных  на фиксированном расстоянии друг от друга). Среди таких алгоритмов:

- по закраске,

- по фокусировке,

- по стереопаре изображений.

Мы рассмотрим алгоритм на основе эпиполярной геометрии. Он включает в себя алгоритм нахождения стереопар, но не требует данных о положении камеры.

Сам по себе алгоритм заключается в поиске локальных особенностей, составлении стереопар и вычислению пространственных координат точек на основе изменения относительного положения точек.

Локальная особенность (или особая точка) – это пиксели с характерной окрестностью, отличающейся от окрестностей других точек. Такими особенностями, как правило выступают рёбра объектов и углы. Локальные особенности описываются набором характеристик, описывающих их окрестность. Существует ряд требований к локальным особенностям:

- инвариантность к повороту,

- инвариантность к масштабированию,

- компактность и эффективность.

Это значит, что дескриптор локальной точки не должен меняться при изменении угла съёмки, масштаба, а также количество таких точек должно быть много меньше количества пикселей.

Распознать локальную особенность можно разными методами, существует множество детекторов с различной чувствительностью, степенью инвариантности,  скоростью работы. Для восстановления сцены как правило используют детекторы, в алгоритме которых уже заложено составление дескриптора (как например SIFT, SURF, ORB), но можно составить свой собственный дескриптор, тогда варианты используемых алгоритмов увеличится (самым распространённым считается детектор углов Харриса).

После нахождения локальных особенностей, нужно сопоставить точки с двух изображений. Этот процесс часто называют стереоотождествлением. Пара изображений при этом называется стереопарой.

Рисунок 1. Стереопара

На следующем шаге нам нужно построить эпиполярные линии для некоторых пар локальных особенностей. Точка в пространстве (найденная на первом шаге) и два центра камер образуют  (точки P, F1, F2) эпиполярную плоскость (далее ЭП). Плоскости изображений пересекают ЭП по эпиполярным прямым. Точки W1, W2, E1, E2 называют эпиполярными полюсами.

Рисунок 2. Эпиполярная геометрия

При этом существует линейное соотношение точки P на плоскостях двух изображений:

                                                                                                            (1)

где , - координаты точки первого и второго изображений соответственно. F – фундаметнальная матрица (далее ФМ).

Компоненты ФМ задаются соотношением:

                                                                                      (2)

где - единичный антисимметричный тензор третьего ранга,  – координаты центров камер,  – компоненты матриц ориентации камер. Эти матрицы могут быть заданы как правые тройки ортонормированных векторов:

                                                                                                            (3)

Матрица камеры может быть определена с точностью до постоянного ненулевого множителя, который не изменит результатов проецирования.

Для фундаментальной матрицы мы можем получить следующий вид:

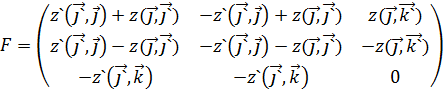                                                                       (4)

где z – расстояние от центра изображения до камеры.

В упрощённом виде мы получаем систему:

                                                                                                       (5)

Здесь X – координаты точки в пространстве. Для решения системы можно векторно умножить первую систему на , вторую - на  и привести к виду AX=0. Тут матрица A имеет размерность 4х4. вспомнив о том, что вектор X – однородные координаты точки, можно его последнюю компоненту прировнять к единице. Тогда получаем систему из трёх уравнений с тремя неизвестными.

Далее изображения ректификацируются, чтобы составить карту глубины для остальных точек. Процесс ректификации – это выравнивание изображений таким образом, чтобы точка одного изображения лежали на эпиполярной линии другого изображения. При этом, выравнивание происходит таким образом, что бы для точки (x0, y0) соответствующая ей эпиполярная линия задавалась уравнением x = x0, в этом случае каждой точки соответствующую ей парную точку нужно искать в той-же строчке втором изображении.

Далее можно найти смещения точек между изображениями. Идея заключается в том, что при перемещении взгляда точки, находящиеся на большем удалении, будут перемещаться медленнее.

Рисунок 3. Вычисление карты глубины

Рисунок 4. Пример ректифицированных картинок, и соответствующей им карты глубины

Стоит отметить, что такой алгоритм хорошо работает на близких объектах.