Применение системы символьных вычислений MAPLE для математического моделирования динамических процессов

Аннотация. В статье рассматриваются возможности использования системы компьютерной алгебры Maple для проведения вычислительного эксперимента, приведены результаты символьных и численных расчетов для решения задачи прикладного характера – определение устой­чивости механической системы простейшего типа из (4n + 1) небесных тел. Показано, что с помощью математического пакета Maple можно проводить сложные и объемные вычисления не только с числовыми, но и с символьными переменными.

Abstract. The article discusses the possibility of using Maple Computer Algebra System for a simulation experiment. The results of symbolic and numerical calculations to solve the problem of applied nature – the determination of the stability of the simple mechanical system of (4n + 1) celestial bodies, are shown. It is shown that the using Maple mathematical software to carry out the big data computations and heavy numerical computing as well as symbolic computing.

Ключевые слова: Maple, прикладная информатика, системы символьных вычислений, вычислительный эксперимент, нелинейные алгебраические уравнения.

Keywords: Maple, applied informatics, symbolic computation systems, simulation experiment, nonlinear algebraic equations.

Введение. Символьная (компьютерная) математика или компью­терная алгебра – большой раздел математического моделирования [1]. Современное конструирование, градостроительство и архитектура, электротехника и множество смежных с ними отраслей, а также процессы обучения по многим техническим дисциплинам активно используют системы автоматизированного проектирования, составной частью которых являются математические пакеты. Рассмотрим возможности компьютерной системы символьной математики Maple для проведения символьных расчетов.

Постановка задачи. Рассматривается упрощенная модель системы из 9 небесных тел (4n + 1 = 9 при n = 2): вокруг большого центрального тела на двух орбитах вращаются менее крупные 8 тел, по 4 тела на каждой орбите. Движение тел осуществляется в одной плоскости (плоскости орбит), поскольку этого достаточно для иссле­дования устойчивости, поэтому координата z не учитывается. На систему накладываются начальные ограничения, обусловленные выбором системы координат: в относительной декартовой системе координат за начало отсчета принимается центральное тело, расстояние между телами на орбитах принимается одинаковым. По заданному критерию необходимо установить, является ли система устойчивой: аналитически определяется равенство всех угловых скоростей тел на орбитах.

Общие уравнения движения тел в системе представлены относи­тельно квадратов угловых скоростей этих тел 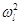 в виде [2]:

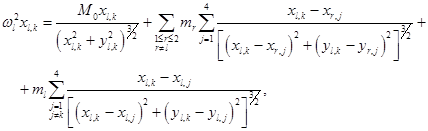
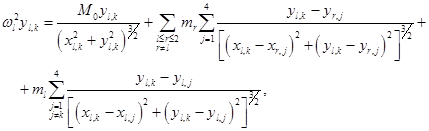                                                                           (1)

где:   k – количество тел на одной орбите (k = 1, 2, 3, 4),

l – количество орбит (l = 1, 2, …),

w_l – частота вращения тел на орбите l,

M₀ – масса центрального тела,

m_r и m_l – массы тел на орбитах, x и y с парными нижними индексами являются координатами тел системы (индексы обозначают номер орбиты и номер тела на ней).

Согласно формулам (1) для системы из 9 тел нужно сформировать и решить систему из нелинейных уравнений и найти величину угловой скорости w в численном виде. Результат округлить до 9-ти знаков после запятой.

Проведение вычислительного эксперимента в среде Maple Используем систему Maple для проведения многочисленных объемных расчетов с символьными и числовыми данными (включая иррацио­нальные величины) данной модели, реализация которых без использова­ния компьютера практически невозможна. Расчеты будут проводиться в среде Maple 13.

Работа на рабочем поле начинается с указания команды restart, которая обнуляет регистры памяти [4]. Выписываем систему уравнений (1) на рабочем поле Maple, представляя уравнения в форме относительно w_l² для каждого значения k и l, поскольку программный код Maple не использует при вычислениях в качестве переменных выражения с алгебраическими операциями. Упрощаем систему, используя подстановки, учитывающие симметричность пар координат из x_lk и y_lk относительно начала координат (рис. 1, уравнение (1)):

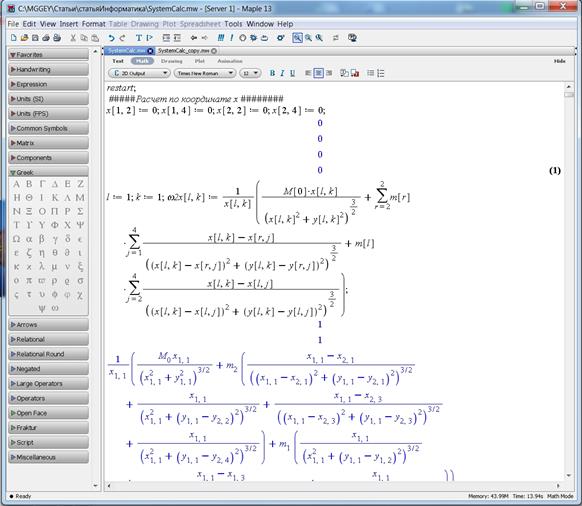
Рисунок 1. Упрощение системы, используя подстановки, учитывающие симметричность пар координат из x_lk и y_lk относительно начала координат (уравнение (1))

Поскольку количество орбит в системе l = 2, а количество небесных тел на каждой орбите k = 4, то из системы уравнений (1) получится 16 уравнений вида:

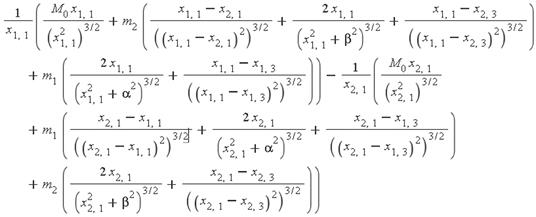
Во время расчетов символьный анализатор Maple учтет вышеуказанные ограничения по координатам (2), и при символьном преобразовании уравнений часть из них обнулится, что приведет к сокращению числа уравнений с 16 до 8. Дальнейшие преобразования с обнулившимися уравнениями будут невозможны: система покажет операцию деления на ноль.

Для дальнейших расчетов полученные выражения частот вращения приравниваются друг к другу попарно. С помощью команды with(combinat) подключаем пакет по разделу комбинаторики [5] и cчитаем количество пар как число комбинаций из 8-ми уравнений по два и получаем 28 уравнений (рис. 2).

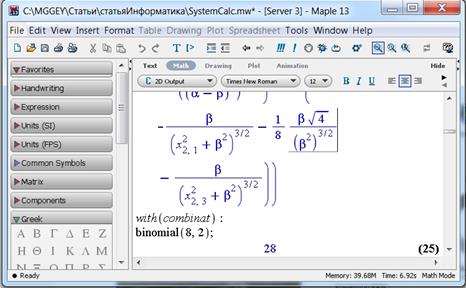
Рисунок 2. Количество пар как число комбинаций из 8-ми уравнений по два и получаем 28 уравнений

Для одной пары выражений приравняем их для двух частот w²_{11 х} и w²_{21 х} через их разность. Аналогично получим оставшиеся 27 сим­вольных выражений.

Учитывая тот факт, что по абсолютному значению существуют только два расстояния (a – радиус большей орбиты, b – радиус меньшей орбиты), вновь упрощаем систему уравнений, заменяя координаты x_lk и y_lk соответствующими им значениями a и b:

x[1, 3] := –a; у[1, 1] := 0; у[1, 2] := a; у[1, 3] := 0;

у[1, 4] := –a; x[1, 1] := a; x[2, 1] := b; у[2, 1] := 0; у[2, 2] := b;                                                                  (3)

у[2, 3] := 0; у[2, 4] := –b; х[2, 3] := –b.

Далее упрощаем все выражения системы с помощью команды collect( ) [4], используемую в цикле, разложив на множители по переменным m₁, М₀ и m₂ (рис. 3).

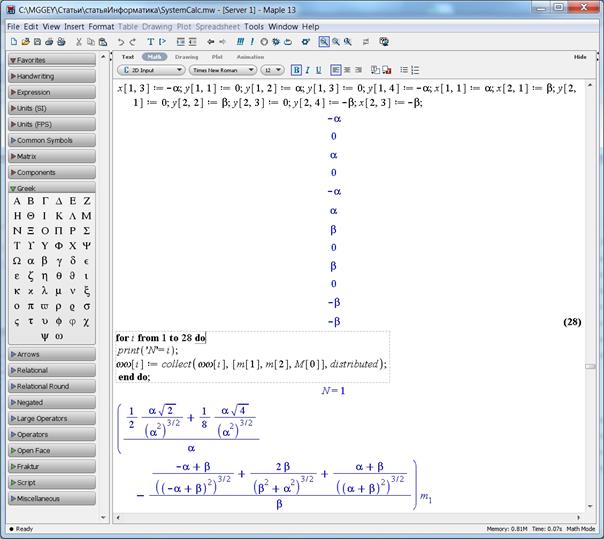
Рисунок 3. Упрощённые выражения

Значение distributed указывает на приведение коэффициентов при членах, содержащих всевозможные произведения степеней неизвестных переменных в списке или множестве, причем суммарная степень всех переменных возрастает от наименьшей к наибольшей. Учитывая тот факт, что количество уравнений системы (их 28) превышает число неизвестных (их всего 5: расстояния a и b и массы m₁, М₀ и m₂.), произ­водим следующее упрощение системы: задаем значения расстояний a и b (в условных единицах, a > b): a := 1.5; b := 1.

Поскольку после преобразований получается система из 28 выра­жений с тремя неизвестными, необходимо найти ранг матрицы системы, чтобы определить возможность существования решения и, при необхо­димости, количество свободных переменных. Для составления матрицы собираем коэффициенты при переменных m₁, М₀ и m₂ со всех 28-ми урав­нений системы (N = 28) при помощи функции coeff(p, х) в цикле [4], которая возвращает коэффициент при х полинома р (рис. 4).

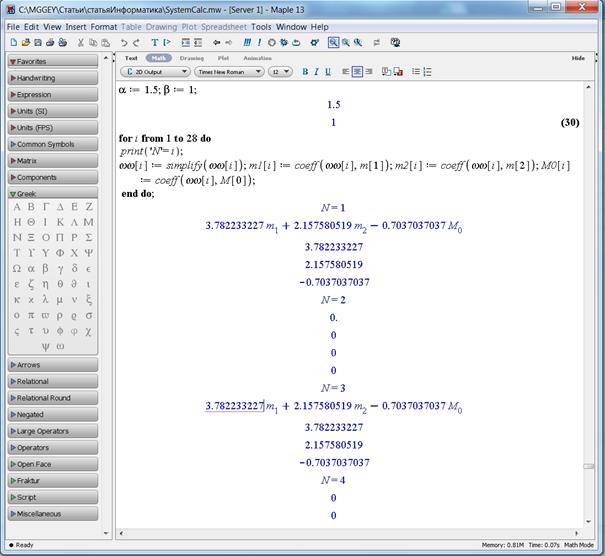
Рисунок 4. Составление матрицы

Команда simplify() упрощает выражение [3], представляя совокупность отношений чисел в виде одного числа, стоящего при переменных m₁, m₂ и M₀. В результате этих преобразований, независимо от исходных значений a и b, некоторые из уравнений обнуляются вследствие сокращения коэффициентов при операциях упрощения, и из исходных 28-ми остается 17 уравнений. Составляем матрицу системы и ищем ее ранг, подключив встроенный пакет MTM, использующий специализированные математические функции: with(MTM): A: = Matrix([ … ]); где после функции Matrix в скобках выписываются элементы матрицы по строкам [4]. Подгрузка пакета осуществляется с помощью команды with, аргументом которой служит имя пакета. Далее, с помощью функции rank(A) ищем ранг полученной матрицы системы A (рис. 5, выражение (32)):

with(MTM): rank(A);

2

Содержимое матрицы больших размеров можно просмотреть в отдельном окне, дважды щелкнув левой кнопкой мыши по матрице, а также выгрузить в файл – электронную таблицу Exce (рис. 5).

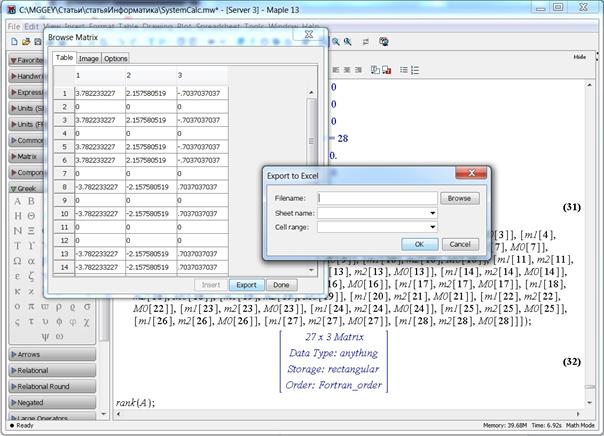
Рисунок 5. Содержимое матрицы больших размеров

Поскольку ранг этой матрицы равен 2, делаем вывод о том, что на следующем этапе преобразований упрощенная система имеет 2 урав­нения с 3-мя переменными (m₁, М₀ и m₂). Необходимо получить эту упрощенную матрицу в явном виде. Используем для этого метод Гаусса, реализованный в Maple с помощью функции gausselim(A), где А – матрица, которую нужно преобразовать. С помощью команды «with(linalg):» подключаем пакет по разделу «Линейная алгебра» для работы с матрицами [5]: with(linalg): A:= gausselim(A) (рис. 6).

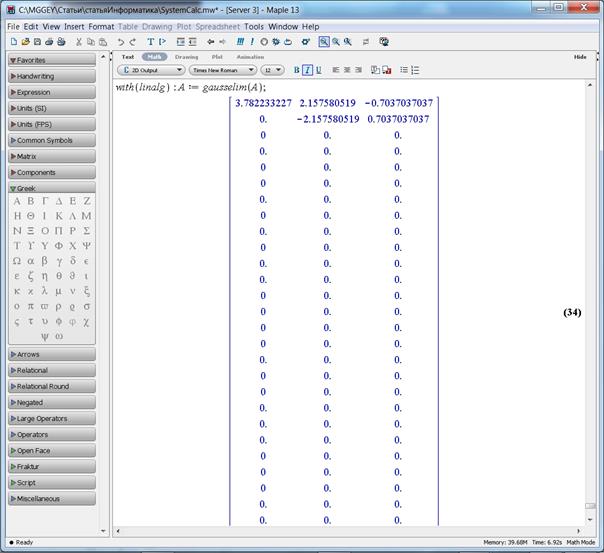
Рисунок 6. Пакет по разделу «Линейная алгебра» для работы с матрицами

По индексам элементов считываем коэффициенты из оставшихся ненулевыми первых двух строк упрощенной матрицы и получаем систему из двух уравнений eqt[1] и eqt[2] для окончательного решения:

a1[1]:= A[1, 1]; a1[2]:= A[1, 2]; a1[3]:= A[1, 3];

a2[1]:= A[2, 1]; a2[2]:= A[2, 2]; a2[3]:= A[2, 3];

eqt[1] := a1[1] m[1] + a1[2] m[2] + a1[3] M[0];

eqt[2] := a2[1] m[1] + a2[2] m[2] + a2[3] M[0];

Приравниваем два оставшихся уравнения, задаем согласно критериям (в условных единицах) значения для двух свободных переменных (масса тел на одной орбите m₁ и масса центрального тела M₀). Получается одно уравнение, решение которого (значение масс тел m₂ со второй орбиты) находим с помощью оператора решения алгебраических уравнений (или систем алгебраических уравнений) – команды solve(u, v) [3], где u – уравнение, v – неизвестная переменная: M[0] := 1; m[1] := 0.5; dd := solve(eqt[1] = eqt[2], m[2]).

Полученная величина m₂ удовлетворяет требуемому условию устойчивости системы тел.

Проверяем правильность решения, подставляя значения перемен­ных в два уравнения системы, округляем результаты до 9-ти знаков в дробной части (присутствие иррациональных чисел в расчетах дает некоторую погрешность) и сравниваем их между собой. Округление осуществляется командами

Float(round(Float(evalf(eqt[1],9)),–9);

Float(round(Float(evalf(eqt[2],9)),–9);

где:   evalf – вычисление значения выражения в численном виде, round – округление к ближайшему целому, Float – указание типа (число с плавающей точкой) округляемого выражения, eqt[1] и eqt[2] – выражения, которые требуется округлить, цифры означают количество знаков в дробной части. Полученные числовые значения выражений eqt[1] и eqt[2] равны между собой (рис. 7, выражение (38)).

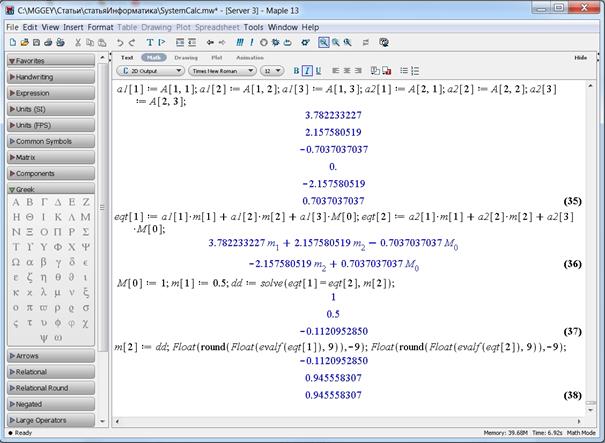
Рисунок 7. Полученные числовые выражения

Таким образом, условие устойчивости механической системы небесных тел выполняется – угловые частоты вращения тел на двух орбитах w₁ и w₂ равны: w₁² = w₂² = 0.945558307 Þ w₁ = w₂, и можно сделать вывод о том, что системы небесных тел с данной структурой существуют и устойчивы. На этом вычислительный эксперимент заканчивается.

Заключение. Среди всех существующих крупных универсальных систем символьных вычислений (MathCad, MatLab, Scientific WorkPlace, Wolfram Mathematica, MuPAD, Maxima/Macsyma и др.), предназначенных для решения задач математического характера, Maple является лидером и по отдельным функциональным характеристикам уступает только пакету Mathematica, традиционно применяющемуся для символьных вычислений. Macsyma имеет проблемы совместимости кодов, сгенерированных в различных версиях. MuPAD не достаточно широко распространен и апробирован. Пакеты Surfer, 3DField и TecPlot предназначены для работы с небольшими объемами данных и не обладают высокой универсальностью, поэтому малоэффективны при расчете сложных функций. Более крупные и многофункцио­нальные пакеты MathCad и MatLab обладают относительно низкой скоростью работы, ограниченный функционал для символьных преобразований и плохо обрабатывают большие объемы информации. По сравнению с Mathematica [1, c. 401-409] Maple является более дружелюбной и открытой системой, использующей в качестве программной среды императивный язык процедурного типа, имеет простой механизм для ведения собственных библиотек и их встраи­ванием в свою программную среду и более удобную справочную систему, что существенно упрощает освоение пакета пользователю, имеющему опыт современного программирования в среде одного из процедурных языков и минимальные сведения по Maple-языку. Синтаксис и организация основных конструкций языка Mathematica существенно отличаются от современных языков программирования, программы менее читабельны, присутствует сложность и избыточность конструкций, исходные тексты стандартных средств скрыты от пользо­вателя, для организации пользовательских библиотек нужно создаваемые собственные средства в полной мере в пакет не интегрируются. Помимо вышеперечисленного, все вышеупомянутые пакеты являются Windows-пакетами, кроме Maple, который является DOS-пакетом, что облегчает восстановление данных из файлов в случае сбоев при работе программы. Также система является в высокой степени кроссплатформенной.

Проведенный с помощью системы Maple вычислительный эксперимент и анализ его результатов показали эффективность данного программного обеспечения для формулировки, решения и исследования различных математических моделей с символьными характеристиками. Показано, что алгебраические средства математи­ческого пакета и применяемый модульный подход программирования, использующий инструменты для символьных вычислений, существенно расширяют диапазон задач учебного и научно-исследовательского направлений, которые могут быть эффективно решены на качественном уровне.

Таким образом, Maple можно считать программным обеспечением, в настоящее время являющимся наиболее удачным для освоения систем символьной компьютерной алгебры в университетах, а также преподавания дисциплин информационно-математического цикла, и наилучшим образом отвечающим задачам образовательного характера: совершенствованию преподавания математически–ориентированных дисциплин, освоения систем компьютерной математики, применения в задачах автоматизации аналитических и численных преобразований, и проведению вычислений в относительно несложных научно-технических проектах.