ИССЛЕДОВАНИЕ ГЕОМЕХАНИЧЕСКОГО СОСТОЯНИЯ БОРТОВ КАРЬЕРА ПУТЕМ ЧИСЛЕННОГО АНАЛИЗА МАССИВА ГОРНЫХ ПОРОД

Аннотация. В статье рассматривается геомеханическое обоснование оптимальных параметров бортов карьера «Западный» месторождения Жайрем на основе численного моделирования. Проведена оценка устойчивости откосов с учетом геологического строения, физико-механических свойств горных пород и воздействия подземных вод. Применение методов численного моделирования позволило определить критические зоны потенциальной неустойчивости и оптимальные углы откосов, обеспечивающие безопасность и эффективность горных работ. Полученные результаты могут быть использованы для прогнозирования деформационных процессов и снижения рисков обрушений при разработке месторождений.

Ключевые слова: геомеханика, устойчивость откосов, численное моделирование, карьер, горные породы.

Для решения ряда инженерных задач в горном деле, помимо качественного описания геомеханических процессов, необходимо их количественное оценивание, которое может быть получено в результате полевых измерений различных проявлений геомеханических процессов или в результате их моделирования. Моделирование имеет преимущество перед натурными измерениями, так как позволяет выявить общие качественные и количественные закономерности геомеханических процессов. Для анализа таких процессов широко применяется математическое моделирование .

В инженерной практике используются различные коэффициенты, определяемые эмпирически на основе полевых наблюдений или данных лабораторных испытаний, для учета факторов, которые невозможно непосредственно включить в расчетную схему. Такой подход приводит к эффекту «накопления ошибок»: проектировщик выбирает значения коэффициентов из определенного диапазона без достаточных оснований, что увеличивает вероятность отклонения полученного результата от истинного значения .

С развитием вычислительной техники в математическом моделировании все чаще применяются численные методы для решения различных инженерных задач в горном деле наряду с традиционными аналитическими методами. Более точное решение задачи может быть получено, если расчетная схема и метод решения позволяют изначально учитывать факторы, представляющие интерес для исследователя. В этом отношении широкие возможности открывают так называемые численные методы, заимствованные из механики деформируемого твердого тела. Наиболее эффективными из них являются метод конечных элементов (МКЭ) и метод предельного равновесия (МПР). Их интенсивное развитие и применение в инженерных расчетах стало возможным благодаря развитию и доступности вычислительной техники .

Одной из программ, реализующих метод конечных элементов и широко используемой для решения задач горного дела, является RS-2, а программное обеспечение «Slide», разработанное компанией Rocscience, реализует метод предельного равновесия. Анализ устойчивости бортов карьера «Дальнезападный» был выполнен методом предельного равновесия в программном комплексе «Slide».

Методы расчета устойчивости, используемые в программном комплексе «Slide»

Один из методов расчета устойчивости бортов карьера заключается в вычислении устойчивости кругло-цилиндрических поверхностей скольжения.

Суть метода заключается в поиске расчетного сечения с минимальным значением отношения горизонтальных проекций удерживающих и сдвигающих сил. Это отношение принимается в качестве расчетного коэффициента запаса устойчивости. Расчетное сечение представляет собой часть откоса, ограниченную снизу заданной круговой дугой скольжения, а сверху – поверхностью откоса. Вертикальные линии делят расчетное сечение на «столбцы» шириной менее одного метра. Силы, действующие на элементарный столбец расчетного сечения, определяются на основе треугольника сил, представленного на Рисунке 1.

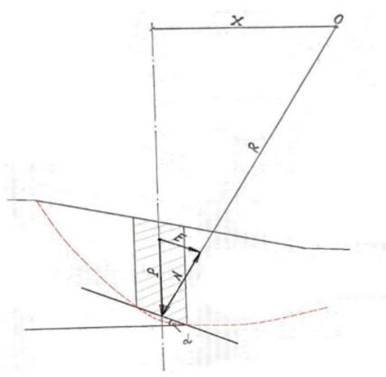
Рисунок 1. Силы, действующие на элементарный столбец расчетного сечения

Напряжения, действующие на поверхность скольжения, обусловлены весом элементарного массива горных пород, выделенного внутри призм возможного обрушения. Сдвигающие и нормальные силы, действующие на эту призму, определяются путем интегрирования элементарных сил вдоль поверхности скольжения. Удерживающие силы рассчитываются с учетом прочностных характеристик горных пород массива в соответствии с теорией предельного равновесия.

Данные программы предназначены для оценки устойчивости цилиндрических и нецилиндрических поверхностей обрушения на скалистых и земляных склонах. Анализ устойчивости поверхностей скольжения выполняется методом предельного равновесия вертикальных блоков, также известным как метод Янбу и Феллениуса. В ходе анализа может быть выбрана отдельная поверхность скольжения, а также использована область центров для определения расположения критических поверхностей в пределах изучаемого объекта. При выполнении расчетов в программы вводятся геометрические параметры борта карьера, а также характеристики горных пород, составляющих массив. Программы используют методы, удовлетворяющие условиям равновесия призмы обрушения и её элементов в предельном состоянии, а также учитывают напряженно-деформированное состояние массива.

Программное обеспечение Slide вычисляет коэффициент запаса устойчивости и строит критическую поверхность скольжения с использованием следующих методов:

• Метод Янбу (Janbu Method)
• Метод Моргенштерна-Прайса (Morgenstern-Price Method)

Все методы предельного равновесия предполагают, что массив грунта над поверхностью скольжения разделен на элементы, а сама поверхность скольжения имеет кругло-цилиндрическую форму.

Метод Янбу. Метод Янбу схож с методом Бишопа, однако учитывает только сумму горизонтальных равновесных сил, не принимая во внимание момент равновесия.

Этот метод учитывает силы, действующие между блоками, а также уравнения равновесия сил в горизонтальном и вертикальном направлениях для всех блоков. При этом уравнение момента равновесия учитывается для всех сечений, кроме последнего, самого верхнего. Коэффициент надежности (FS) определяется путем нахождения направления сил, действующих между блоками, после чего вычисляются значения этих сил.

Метод Моргенштерна-Прайса. Этот метод также учитывает взаимодействие сил между блоками. Однако результирующие сдвигающие и удерживающие силы, действующие между блоками, имеют разные направления в каждом блоке (полусинусоидальная функция). Метод Моргенштерна-Прайса является более точным, так как учитывает три уравнения равновесия:

• уравнения равновесия сил в горизонтальном и вертикальном направлениях,
• уравнение момента равновесия.

Коэффициент надежности (FS) в этом методе определяется путем решения уравнения сил, действующих между блоками.

Метод Феллениуса. Классический блочный метод (метод Феллениуса) применяется для неоднородных откосов и горных массивов, обладающих сцеплением и углом внутреннего трения, где поверхность скольжения можно аппроксимировать окружностью. Этот метод удобен для сложных расчетов, однако он менее точен при анализе напряженного состояния массива с высоким поровым давлением.

Расчет устойчивости бортов карьера методом предельного равновесия

Первоначальный анализ месторождения «Жайрем» был проведен с учетом чувствительности параметров. В рамках этого подхода изменялись различные исходные параметры для построения графика, который позволяет оценить отклонения и их влияние на общий коэффициент устойчивости.

Сравнение пропорциональных соотношений в модели с реальными свойствами массива показало лишь незначительные отклонения в прочности, интенсивности трещиноватости и морфологии нарушений. Это свидетельствует о том, что Западный и Дальнезападный участки можно рассматривать как однородный массив в рамках геомеханического анализа, без необходимости их разделения.

Программное обеспечение Slide анализирует устойчивость поверхностей скольжения с использованием методов предельного равновесия как для вертикального, так и для наклонного сечения. Возможно проведение анализа отдельных поверхностей скольжения, а также применение методов поиска для определения критической поверхности скольжения для заданного откоса.

Далее, на Рисунке 2 представлены результаты расчетов, выполненных методом предельного равновесия в программном комплексе Slide.

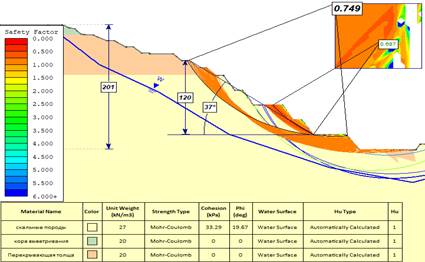
Рисунок 2. Результаты численного анализа по сечению

Результаты геомеханического моделирования методом предельного равновесия приведены в таблице 1.

Согласно результатам численного анализа, можно увидеть, что массив горных пород в восточной части карьера находится в неустойчивом состоянии, тогда как западная сторона карьера в целом стабильна. Восточная сторона карьера «Дальнезападный» спроектирована с более крутым общим углом, чем западная сторона, что привело к потере устойчивости массива горных пород по результатам численного анализа методом конечных элементов.

Таблица 1.

 Результаты численного анализа методом предельного равновесия

На основе анализа физико-механических свойств массива горных пород, результатов ранее проведённых геомеханических исследований и численного анализа, выполненного методом предельного равновесия, построена логарифмическая зависимость изменения коэффициента запаса устойчивости от изменения общего угла и высоты откоса.

Логарифмическая зависимость построена методом наименьших квадратов, основанным на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных.

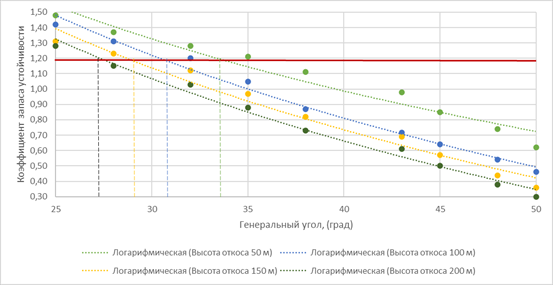
Рисунок 3. График зависимости коэффициента запаса устойчивости (КЗУ) от общего угла и высоты откоса

Заключение

1. Проведен детальный анализ ранее выполненных исследований по определению физико-механических свойств горных пород и устойчивости бортов карьера «Дальнезападный» с целью получения более достоверных данных о структурных особенностях и прочностных характеристиках массива.

2. На основе численного моделирования методом предельного равновесия выполнен анализ устойчивости бортов карьера «Дальнезападный». В ходе анализа программное обеспечение рассчитало коэффициенты запаса устойчивости и построило критические поверхности скольжения (призму обрушения) с использованием метода Бишопа.

3. В результате анализа данных, полученных в ходе компьютерного моделирования, и аналитического метода наименьших квадратов построен график, позволяющий определить значение коэффициента запаса устойчивости в зависимости от изменения общего угла и высоты откоса.

Практическое применение данного исследования возможно в следующих отраслях промышленности: горнодобывающей отрасли, информационных технологиях.