Расчет линейной цепи синусоидального тока

В современном мире широко распространены разнообразные по форме переменные токи и напряжения: синусоидальные, прямоугольные, треугольные и др. Значение тока, напряжения, ЭДС в любой момент времени t называется мгновенным значением и обозначается малыми строчными буквами, соответственно:

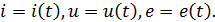
Токи, напряжения и ЭДС, мгновенные значения которых повторяются через равные промежутки времени, принято называть периодическими, а наименьший промежуток времени, через который эти повторения происходят, называют периодом Т.

Если кривая изменения периодического тока описывается синусоидой, то ток называют синусоидальным. Если кривая отличается от синусоиды, то ток несинусоидальный.

В основном электрическая энергия производится, передается и расходуется потребителями в виде синусоидальных токов, напряжений и ЭДС [1].

В данной работе выполним расчет линейной цепи синусоидального тока, схема которой изображена на рисунке 1.

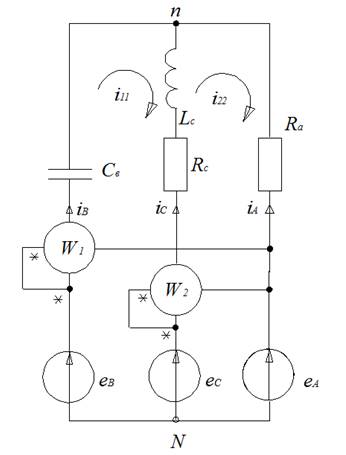
Рисунок 1. Схема электрической цепи

В цепи, изображенной на рисунке 1, действуют источники напряжения с ЭДС, изменяющимися во времени по закону:

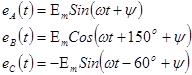
Параметры ЭДС 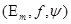 и параметры элементов схемы (R, C, L) приведены в таблице 1.

Таблица 1.

Параметры ЭДС и элементов электрической схемы

Расчет электрической цепи выполним следующим образом:

1.    Построим временные характеристики e_A(t), e_B(t), e_C(t);

2.    Рассчитаем схему методами контурных токов и межузловых напряжений.

Построение временных характеристик электрической цепи

Для построения временных характеристик (графиков) ЭДС получим аналитические выражения для них:

e_A(t)=250sin(ωt -55º)B,

e_B(t)=250cos(ωt+150º-55º)=250 sin(ωt+150º-55º+90º)=250sin(ωt - 175º)B,

e_C(t)=- 250sin(ωt-60º-55º)=250 sin(ωt 115º+180º)=250sin(ωt +65º)B.

Графики e_A(t),e_B(t) и e_C(t) приведены на рисунке 2.

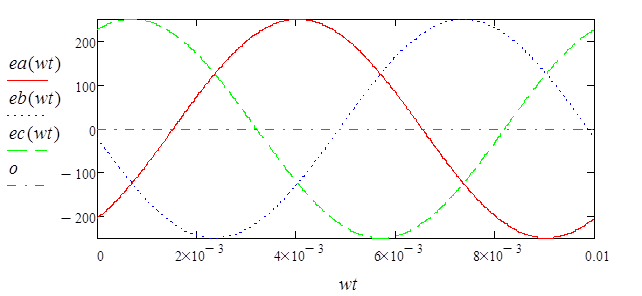
Рисунок 2. Времнные характеристики электрической цепи

Расчет электрической схемы методом контурных токов и межузловых напряжений

Запишем комплексы действующих значений ЭДС:

.

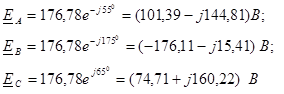Находим комплексные сопротивления ветвей схемы.

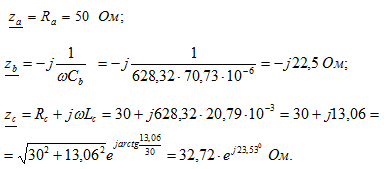
Запишем уравнения по второму закону Кирхгофа для контурных токов в матричной форме:

Подставим числовые значения:

Или

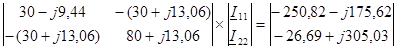
Определитель системы:

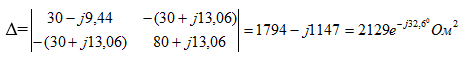
Алгебраические дополнения:

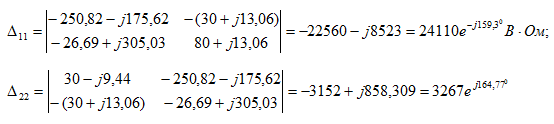
Находим комплексы контурных токов:

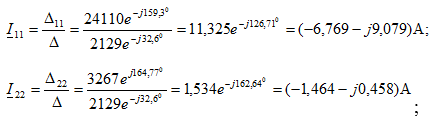
Вычислим комплексы токов ветвей:

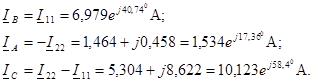
Для расчета той же схемы методом межузловых напряжений находим комплексное значение напряжения смещения нейтрали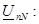 

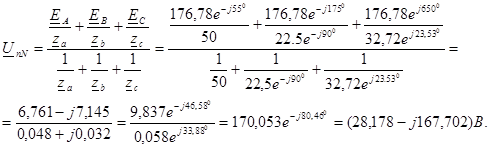
Вычислим комплексные значения токов ветвей, пользуясь законом Ома:

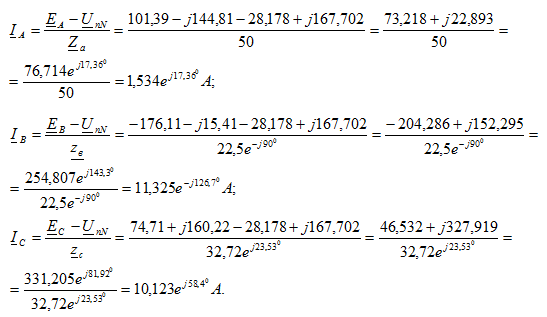
Таким образом, были построены характеристики электрической цепи и был произведен расчет рассматриваемой электрической схемы методами контурных токов и межузловых напряжений.