LEVENSHTEIN ALGORITHM AND ITS APPLICATION IN TEXT ANALYSIS

The ever-increasing volume of textual information necessitates the development of new and the improvement of existing methods for its analysis and processing. One of the key tools in the field of text analysis is the Levenshtein algorithm, which is widely used for comparing texts, correcting typos, text auto-replacement, and other tasks.

The purpose of this work is to investigate the Levenshtein algorithm, analyze its efficiency, advantages, and limitations for various models.

"The Levenshtein algorithm, also known as edit distance, is a method for measuring the difference between two character strings. It determines the minimum number of insertion, deletion, or substitution operations required to transform one string into another. This algorithm is used for string comparison, typo correction, autocorrection, and other text processing tasks"[1].

The principle of the Levenshtein algorithm is based on dynamic programming. The main stages of the algorithm include:

a) Initialization: Creating a matrix of size (m+1) × (n+1), where m and n are the lengths of the strings being compared. At the first stage, the matrix is filled with values from 0 to m and from 0 to n.

b) Matrix Filling: The matrix values are computed using a recurrence formula that considers the cost of insertion, deletion, and substitution operations. Each cell of the matrix represents the minimum edit distance for the corresponding prefixes of the strings.

c) Distance Determination: The value in the bottom-right corner of the matrix represents the sought edit distance between the two strings[1].

Mathematically, the Levenshtein algorithm is defined as the minimum number of edit operations required to transform one string into another.

Let s1 ​and s2 ​denote the strings to be compared. Let d (i,j) be the edit distance between the prefixes of the strings s1​ [1..i]and s2 ​[1..j]. Then the value of d (i,j) is computed as follows:

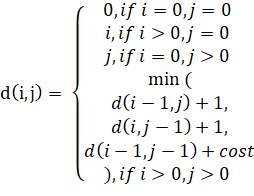
The variable cost represents the expense of an edit operation (character insertion, deletion, or substitution). These mathematical principles formalize the Levenshtein algorithm's operation, enabling its use for comparing and analyzing textual data in various applied contexts.

During the research, the Levenshtein algorithm was implemented within the mobile application "AKVT.Schedule" to process user input. The implementation utilized the Dart programming language [2,3,4].

The initial experiment employed a basic approach where a fixed, identical error tolerance was applied to all text inputs. This resulted in inaccurate sorting of the results.

To resolve this problem, an enhanced method was developed. It calculates the allowable number of errors as a percentage of the string's length, allowing for more precise similarity assessment for strings of different sizes.

This improved technique demonstrated higher accuracy in comparing strings and identifying textual similarities, thereby increasing the algorithm's overall effectiveness for text analysis tasks.

The Levenshtein algorithm offers significant advantages, including high precision, ease of implementation, versatility, and computational efficiency, making it a vital tool for textual analysis.

However, the algorithm also has limitations. It can be inefficient when processing very long strings or large datasets. Furthermore, it does not account for contextual meaning or semantics, which may lead to inaccuracies in certain scenarios.

To address these constraints, more sophisticated methods considering context and semantics could be developed. Opportunities also exist for optimizing the algorithm to handle extensive data volumes and lengthy strings more effectively.