ИССЛЕДОВАНИЕ ТОЧНОСТИ ПОЗИЦИОНИРОВАНИЯ В СПУТНИКОВОЙ ГЕОДЕЗИИ С УЧЕТОМ ФИЗИЧЕСКИХ СВОЙСТВ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

PHYSICS OF ELECTROMAGNETIC WAVE PROPAGATION IN SATELLITE GEODESY

Rozhkov Evgeniy Alexandrovich

Candidate of Technical Sciences, Docent of the Department of Physics, Kuban State Agrarian University named after I. T. Trubilin, Russia, Krasnodar

Gaityan Elizaveta Arsenovna

Student of the Faculty of Land Management, Kuban State Agrarian University named after I. T. Trubilin, Russia, Krasnodar

Аннотация. В данной статье рассматриваются физические основы распространения электромагнитных волн в системах спутниковой геодезии. Особое внимание уделено влиянию вращения Земли на точность определения расстояний при распространении и отражении сигнала между спутником и поверхностью Земли. Предложена упрощенная расчетная модель, которая позволяет оценить разность длин пути электромагнитной волны и соответствующую погрешность позиционирования в зависимости от высоты орбиты спутника. Целью работы является количественная оценка систематической погрешности, возникающей из-за смещения точки приема за время прохождения сигнала. На основе геометрической модели, учитывающей зависимость радиуса Земли от широты, рассчитана величина этой погрешности для различных высот орбит (2000, 10000 и 30000 км) и географических точек (Сингапур, Краснодар, Москва, Мурманск). Результаты показывают, что ошибка прямо пропорциональна высоте орбиты, достигая десятков метров, и слабо зависит от широты. Авторы делают вывод о необходимости учета данного эффекта и его аппаратно-алгоритмической компенсации для достижения высокой точности в современных спутниковых навигационных системах.

Abstract. This article discusses the physical basis of electromagnetic wave propagation in satellite geodesy systems/ Special attention is paid to the effect of the Earth’s rotation on the accuracy of determining  distances during propagation and reflection of the signal between the satellite and the Earth’s surface/ A simplified computational model is proposed that makes it possible to estimate the difference in the path lengths of an electromagnetic wave and the corresponding positioning error depending on the height of the satellite’s orbit. The aim of the work is to quantitatively assess the systematic error arising from the displacement of the reception point during the signal's transit time. Based on a geometric model that accounts for the dependence of the Earth's radius on latitude, the magnitude of this error is calculated for various orbital altitudes (2000, 10000, and 30000 km) and geographical locations (Singapore, Krasnodar, Moscow, Murmansk). The results show that the error is directly proportional to the orbital altitude, reaching tens of meters, and depends only weakly on latitude. The authors conclude that it is necessary to account for this effect and its hardware-algorithmic compensation to achieve high accuracy in modern satellite navigation systems.

Ключевые слова: спутниковая геодезия, электромагнитные волны, распространение сигнала, вращение Земли, точность позиционирования.

Keywords: satellite geodesy, electromagnetic waves, signal propagation, Earth rotation, positioning accuracy.

Спутниковая геодезия – одно из наиболее эффективных и распространенных методов определения пространственного положения объектов на земной поверхности. Её развитие стало возможным благодаря использованию глобальных навигационных спутниковых систем, принцип работы которых основан на измерении времени прохождения радиосигнала от спутника до приёмника на поверхности Земли. При этом точность напрямую определяется корректностью учета физических факторов, влияющих на скорость и траекторию распространения сигнала [1, 2]. Одним из таких факторов является вращение Земли, что приводит к изменению взаимного положения спутника и отражающей точки поверхности за время прохождения сигнала. Даже при малых временных интервалах это смещение может вносить значительные погрешности в расчет расстояний, особенно для высокоточных геодезических измерений.

Целью настоящего исследования является комплексная оценка и количественный анализ предельной точности позиционирования в спутниковых геодезических системах, определяемой фундаментальными физическими свойствами распространения электромагнитных волн в атмосфере Земли и космическом пространстве.

Электромагнитные волны представляют собой распространяющееся в пространстве возмущение электрического и магнитного полей. В вакууме они распространяются со скоростью света, но в условиях земной атмосферы они зависят от физических свойств среды [3, 4]. Для спутниковой геодезии используются радиосигналы диапазона ультракоротких волн, что обеспечивает их устойчивое распространение и высокую точность измерений.

При прохождении через неоднородную среду электромагнитные волны испытывают преломление и замедление, что приводит к увеличению времени распространения сигнала. Данные эффекты оказывают существенное влияние на точность временных и фазовых измерений, используемых в спутниковой геодезии.

Нельзя оставить без внимания и влияние ионосферы и тропосферы. Ионосфера является верхней областью атмосферы планеты, содержащая высокую концентрацию свободных ионов и электронов, которые оказывают дисперсное воздействие на радиосигналы. Ионосферная задержка зависит от частоты электромагнитной волны и может значительно изменятся в зависимости от солнечной активности и времени суток. Данный эффект является одним из основных источников погрешностей при спутниковых измерениях. В то время как тропосфера- нижний слой атмосферы, оказывает недисперсионное влияние на электромагнитные волны. Тропосферная задержка обусловлена изменением показателя преломления воздуха, который зависит от температуры, давления и влажности. Несмотря на меньшую изменчивость, тропосферные эффекты также требуют обязательного учета при высокоточных геодезических измерениях.

Существенное влияние на качество спутниковых измерений оказывает эффект многопутности. Он возникает при отражении электромагнитных волн от земной поверхности и искусственных объектов. Отраженные сигналы искажают измерения и приводят к снижению точности определения координат объектов, особенно в условиях плотной застройки территории [5].

Для снижения влияния физических факторов в спутниковой геодезии применяют методические решения и аппаратурное обеспечение. Так же для современной геодезии свойственно применение глобальной модели ионосферы, например, NeQuick, IRI-Plas, уточняемые в реальном времени по данным ГЛОНАСС/ GPS. Данные модели предназначены для вычисления концентрации электронов в атмосфере [6, 7]. На основе этих данных можно компенсировать задержку сигнала и повысить точность проводимых измерений.

Спутники находятся на разных орбитах в зависимости от их назначения. Рассмотрим основную классификацию по высоте. Существуют спутники на низкой околоземной орбите, которые находятся на высоте от 160 км до 2 000 км над поверхностью Земли. На такой высоте используются МКС, научные и военные спутники, спутники связи (Starlink, OneWeb, Iridium), спутники дистанционного зондирования Земли.

Навигационные системы (GPS, ГЛОНАСС, Galileo, BeiDou) вращаются на средней околоземной орбите (от 2 000 км до 35 786 км) с периодом обращения от 2 до 24 часов. Важную роль играют спутники на геостационарной орбите, которая составляет 35 786 км точно над экватором. Их период обращения ровно 24 часа (синхронизирован с вращением Земли). Спутник "висит" над одной точкой планеты. На такой высоте находятся телекоммуникационные спутники (телевидение, интернет).

Также в настоящее время существуют спутниковые системы, способные находиться на высокой эллиптической орбите, у которых высота в апогее составляет до 400 000 км. Это в основном спутники связи для высоких широт ("Молния", "Тундра").

Наибольший интерес для спутниковой геодезии представляет средняя орбита, так как она позволяет с достаточной точностью определять положение объектов и проводить необходимые расчеты. Современные чипы в смартфонах и приемниках почти всегда используют сигналы всех видимых спутников сразу (GPS + ГЛОНАСС + Galileo + BeiDou). Это называется multi-GNSS. В таком режиме реальная точность обычно составляет 2-4 метра в благоприятных условиях (открытое небо). Такие погрешности связаны с тем, что скорость распространения электромагнитных волн хоть и велика и составляет 300 000 км/с, однако она конечная и за время прохождения сигнала по атмосфере Земли и при отражении, позиционируемая точка успевает повернуться на некоторый угол, который и определяет погрешность.

Рассмотрим 3 базовых случая, когда спутник находится на высоте 2000 км, 10000 км и 30000 км и рассчитаем точность определения положения объекта. Положение объекта возьмём следующим образом: г. Сингапур на экваторе (0° широты), г. Краснодар (45° северной широты), г. Москва (55° северной широты), г. Мурманск (67° северной широты).

Время распространения электромагнитной волны от спутника и обратно, рассчитаем по формуле:

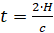 ,                                                                                                          (1)

где H – высота орбиты спутника, км; c – скорость света, которая в атмосфере принимается равной 299 700 000 м/с.

Радиус Земли не постоянен, и его зависимость от широты — ключевой момент в геодезии, навигации и картографии. Земля представляет собой сфероид (эллипсоид вращения), сплюснутый у полюсов и расширенный на экваторе.  Для расчета расстояния, пройденного точкой за время распространения электромагнитной волны, возьмем радиус кривизны в первом вертикале, который рассчитывается по формуле:

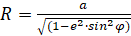  ,                                                                                                 (2)

где a – большая (экваториальная) полуось: 6 378 137 км; e² – квадрат первого эксцентриситета эллипсоида (берется за 0.00669437999014); φ – геодезическая широта, рад.

Линейную скорость точки на данной широте можно рассчитать по формуле:

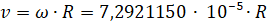 ,                                                                             (3)

где ω – угловая скорость Земли (берется за 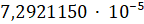), рад/с.

Расстояние, на которое отклонилась точка за время распространения электромагнитной волны (точность позиционирования) можно определить по формуле:

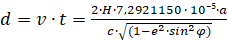                                                                                   (4)

Используя данную формулу, произведем расчеты для начальных параметров и результаты сведем в таблицу 1.

Таблица 1.

Результаты вычисления точности позиционирования в зависимости от высоты геодезического спутника и местоположения объекта

Проводя анализ полученных результатов, можно утверждать, что точность позиционирования во многом определяется высотой орбиты спутника и не сильно зависит от местоположения объекта на поверхности Земли.  Наиболее оптимальным будет выбор высоты геодезического спутника от 2000 до 10000 км. Большая высота дает значительную погрешность, которую необходимо учитывать при геодезических расчетах.

Вращение Земли вносит метрологически значимый вклад (от единиц до десятков метров) в общую погрешность спутникового позиционирования. Величина этого вклада прямо пропорциональна высоте орбиты и слабо возрастает с широтой. В современных высокоточных геодезических системах данный эффект успешно компенсируется на аппаратно-алгоритмическом уровне, что является необходимым условием для достижения сантиметровой и даже миллиметровой точности измерений. Проведенный расчет подтверждает необходимость учета динамики Земли как целостной физической системы при проектировании и эксплуатации глобальных навигационных спутниковых систем.