ПРОСТОЙ МЕТОД РЕШЕНИЯ ОДНОЙ ЗАДАЧИ С ПАРАМЕТРОМ И МЕТОДИКА СОСТАВЛЕНИЯ РАЗЛИЧНЫХ ЕЕ ВАРИАЦИЙ

Задача с параметром из года в год остается одной из самых трудных проблем для школьников, так как для их понимания и успешного решения необходим достаточный уровень владения математическими определениями, свойствами и теоремами. В работе рассмотрим решение задачи из представленного ниже семейства задач с параметром, доступное для решения среднему ученику с помощью элементарных школьных знаний.

Задача 0. Найти все значения параметра , при которых уравнение:

, где 

а) не имеет корней;

б) имеет один корень;

в) имеет более одного корня;

г) имеет хотя бы один корень.

Данная формулировка задачи в общем виде может служить алгоритмом для составления учителем различных вариантов данной задачи для учеников, а также инструментом для самих школьников при подготовке к ЕГЭ по математике профильного уровня.

Рассмотрим конкретную задачу с параметром данного семейства, решение которой приводится на сайте «Решу ЕГЭ» (Д.Д. Гущина) с помощью аналитического метода, ориентированного на сильных и одаренных учеников. Он заключается в исследовании двух монотонно возрастающих функций. [1]

Для этой же задачи представим легкодоступный метод решения, опирающийся на материал школьных учебников базового уровня.

Задача 1. Найдите все значения , при каждом из которых уравнение

имеет более одного корня. [1]

Решение:

Преобразуя данное уравнение , получим:

Используя формулу сокращенного умножения для разности кубов [2, с.183], имеем:

Вынесем множитель  за скобки и получим:

Полученное уравнение равносильно совокупности двух уравнений:

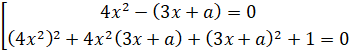
Используя утверждение, что сумма положительных и неотрицательных выражений всегда положительна, покажем, что левая часть второго уравнения строго больше нуля. Для этого два первых слагаемых дополним до полного квадрата.

Таким образом, второе уравнение не имеет действительных корней. Тогда первое уравнение нашей совокупности, должно иметь более одного корня, т.е. два различных корня. Для этого дискриминант .

Ответ: _.

Замечание. Рассмотренную в статье задачу с параметром можем усложнить для школьников, увлекающихся изучением математики.

Задача 2. Найдите все значения a, при каждом из которых уравнение

имеет три различных корня.

Таким образом, задача, не теряя свою ключевую идею решения, становится более интересной для исследования учениками, что также позволяет применить школьное понятие определения модуля.

Работа может быть полезна как для школьников при подготовке к единому государственному экзамену по математике профильного уровня, так и для учителей, а также студентов, интересующихся решением задач с параметрами.