Математическое моделирование процесса фильтрования с образованием несжимаемого осадка

В связи с высоким темпом развития технологий, в особенности автотранспорта и промышленных предприятий, возрастает всё большая необходимость соблюдения экологического баланса между техникой и природой. Одной из ступеней этого баланса является защита окружающей среды путём очистки промышленно-ливневых сточных вод от взвешенных веществ и нефтепродуктов. Защита водных ресурсов является одной из первостепенных задач сохранения городской природной среды.

Сточная вода поступает через общесплавную канализацию на городские очистные сооружения, которые предназначены для очистки поверхностных и близких к нему по составу производственных стоков. При этом загрязненная вода проходит несколько этапов очистки. На стадии доочистки осуществляется процесс фильтрования в специальном техническом оборудовании – фильтре.

Скорый механический фильтр предназначен для очистки промышленно-ливневых сточных вод от взвешенных частиц и нефтепродуктов, оставшихся в осветленной воде после отстаивания. После забивки пор в скором фильтре необходимо проводить его регенерацию, назначение которой состоит в том, чтобы разрушить плёнку нефтепродуктов и удалить задержанные в процессе фильтрования загрязнения. Для наглядного примера на рисунке 1 изображена схема очистки сточных вод на стадии фильтрования, применяемая на Котляково-Коломенских очистных сооружениях, входящих в состав МГУП «Промотходы».

Рисунок 1. Схема очистки сточных вод на стадии фильтрования: 1 – резервуар осветленной воды; 2, 5 – насосы; 3 – ультразвуковой расходомер; 4 – резервуар воды для промывки фильтра; 6 – резервуар очищенной воды; 7 – резервуар промывных вод; 8 – скорый фильтр

Из резервуара осветлённой воды (1) насосом (2) вода подается на доочистку в фильтр (8). Профильтрованная вода собирается в резервуаре очищенной воды (6). Часть очищенной воды с помощью насоса(5) используется для промывки фильтра(4), а остальная вода для других нужд предприятия (7) [3, с. 15].

От регенерации фильтра напрямую зависит себестоимость очистки промышленно-ливневых сточных вод. Для того чтобы снизить расходы, необходимо спрогнозировать работу скорого фильтра так, чтобы обслуживающий персонал имел представление о том, в какой момент времени необходимо прекратить процесс фильтрования и начать регенерацию фильтрующей загрузки.

Работу фильтра необходимо останавливать, когда рост перепада давления, из-за образующегося осадка и закупоривания пор нефтепродуктами, достигает критического значения, при котором скорость фильтрования значительно снижается, а сам процесс становится не выгодным из-за увеличения энергетических затрат [1, с. 169]. В связи с этим требуется знать гидравлические характеристики в новых условиях эксплуатации скорого механического фильтра для его правильной работы, а именно, удельное сопротивление осадка и сопротивление фильтрующей поверхности.

Рассмотрим процесс фильтрования с образованием несжимаемого осадка на несжимаемой перегородке в дифференциальном уравнении (1):

 ,                                                                                                 (1)

где: V – объем фильтрата, м³;

S – поверхность фильтрования, м²;

τ – продолжительность фильтрования, сек;

∆P – разность давлений, н∙м^-2;

µ – вязкость жидкой фазы суспензии, н∙сек∙м^-2;

r₀ –удельное объемное сопротивление осадка, м^-2;

x₀ – отношение объема осадка к объему фильтрата, м³∙м^-3;

R_ф.п. – сопротивление фильтровальной перегородки, м^-1.

Для несжимаемых осадков и перегородок в уравнении (1) величины r_0, x₀ и R_ф.п. постоянны и, следовательно, не зависят от изменения величины ∆P.

При интегрировании уравнения (1) необходимо принимать во внимание условия процесса фильтрования, который может протекать при постоянной разности давлений, постоянной скорости, постоянных разности давлений и скорости и переменных разности давлений и скорости.

Уменьшение скорости фильтрования при постоянной разности давлений и возрастание разности давлений при фильтровании с постоянной скоростью обусловлены повышением сопротивления осадка в результате увеличения его толщины [2, c. 27–28].

Для решения в общем виде уравнения фильтрования при переменной разности давлений и одновременно при переменной скорости примем, что сопротивлением фильтровальной перегородки можно пренебречь. При этом условии основное дифференциальное уравнение фильтрования (1) примет вид:

 ,                                                                                                        (2)

где:  – переменная разность давления, н∙м^-2.

Из уравнения (2) получим:

 ,                                                                                                     (3)

Здесь постоянная

                                                                                                            (4)

Интегрируя уравнение (3) в пределах от 0 до V и от 0 до t, получим:

                                                                                                  (5)

Интеграл правой части последнего уравнения можно найти, если известно аналитическое или графическое функции  (см. рис 2).

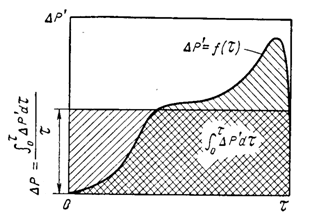
Рисунок 2. Графическая интерпретация уравнения (8) [2, c. 30–31]

Преобразовав зависимость (5) можно получить удельное объемное сопротивление осадка при ∆Р=var:

                                                                                                        (6)

Рассмотрим эквивалентный процесс фильтрования, описанный выше, при постоянной разности ∆Р=const.

Эквивалентность обоих процессов может быть достигнута если за одно и то же время t получится одинаковое количество фильтрата V.

Подставим постоянное значение  в уравнение (5):

,                                                                                                   (7)

Откуда:

                                                                                                     (8)

Для нахождения удельного объемного сопротивления осадка при ∆Р=const подставим уравнение (7) в уравнение (5) и получим следующее выражение (9):

                                                                                                    (9)

Существующие методики, используемые для расчета оборудования, не учитывают наличия нефтепродуктов в воде, поступающей на фильтрацию. Моделирование процесса фильтрования в лабораторных условиях не может дать такого результата, как при заводских испытаниях, так как воссоздать физико-химические параметры жидкости поступающей на очистку крайне сложно. Для этого необходимо проводить промышленные эксперименты.

В данной работе были рассмотрены два схожих процесса и зависимости для определения удельного сопротивления несжимаемого осадка, которые могут быть полезны для решения ряда практических задач. Снятие гидравлических характеристик существующего оборудования необходимы для разработки системы прогнозирования работы безнапорного скорого фильтра.