К вопросу формирования у обучающихся 5 класса УУД при обучении математике на основе использования возможностей компьютерной системы «Живая математика»

Аннотация. В статье актуализируется проблема формирования универсальных учебных действий при обучении математике у обучающихся 5 класса. Представлен опыт формирования УУД у обучающихся 5 класса посредством использования компьютерной системы «Живая математика».

Ключевые слова: Компьютерная система «Живая математика», универсальные учебные действия, формирование универсальных учебных действий, обучение математике в 5 классе.

Федеральные государственные образовательные стандарты основного общего образования определили новые требования к метапредметному результату обучения школьников. В состав этих требований включены универсальные учебные действия (УУД) школьников: познавательные, регулятивные и коммуникативные. Трудно переоценить роль и значение способности и готовности школьников к выполнению этих действий как для обучения, так и для самообразования в течение всей жизни.

Появление прикладного программного обеспечения нового поколения позволяет расширить область применения информационных технологий в учебном процессе, расширить методические горизонты при обучении математике в школе. К этой группе программного обеспечения относятся универсальные математические пакеты символьных, численных вычислений и геометрических построений – так называемые системы компьютерной математики [Плясунова, 2004].

Под системами компьютерной математики (СКМ) будем понимать комплексные программные средства, обеспечивающие автоматизированную, технологически единую и замкнутую обработку задач математической направленности при задании их условий на специально предусмотренном языке пользователя [Зайцева, 2005, с. 40].

Системы компьютерной математики обладают богатым набором инструментов для построения анимационных чертежей. Они удобны и просты в использовании. Для учителя СКМ представляет собой ансамбль инструментов, с помощью которых можно добиваться разнообразных педагогических целей. Для обучаемого – это среда обитания, «населенная» многочисленными разнотипными инструментами, многие из которых имеют индивидуальные настройки [Экспериментальная математика, 2016].

Исследования, проведенные С.А. Дьяченко [Дьяченко, 2000], показывают, что среди достоинств применения компьютера в обучении математике можно отметить следующие: возможность наглядного представления графических данных; быстроту и точность вычислений; разнообразие способов предъявления учебной информации; возможность конструирования анимационных компьютерных моделей математических объектов и проведения, на их основе, компьютерных экспериментов и исследований; расширение комплекса учебных задач; повышение информационной культуры и активизация учебно-познавательной деятельности обучающихся.

Наиболее ярким представителем компьютерной математики является система динамической геометрии «Живая математика».

В данной статье представим опыт использования компьютерной системы «Живая математика» в процессе обучения математике учащихся 5 классов, с целью формирования регулятивных УУД.

Важное место в формировании умения учиться занимают регулятивные универсальные учебные действия, обеспечивающие организацию, регуляцию и коррекцию учебной деятельности. Поэтому поиск инновационных технологий и методов обучения, использование которых способствует формированию регулятивных УУД при обучении предмету, является одной из приоритетных задач математического образования школьников.

К регулятивным УУД относят следующие группы действий:

• целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно;
• планирование – определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий;
• прогнозирование – предвосхищение результата и уровня усвоения, его временных характеристик;
• контроль – в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
• коррекция – внесение необходимых дополнений и корректив в план и способ действия в случае расхождения эталона, реального действия и его продукта;
• оценка – выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.
• волевая саморегуляция как способность к мобилизации сил и энергии; способность к волевому усилию – к выбору в ситуации мотивационного конфликта и к преодолению препятствий [Гаврилова, 2013].

Компьютерная система динамической геометрии «Живая математика» позволяет формировать у обучающихся основы регулятивных УУД посредством специальных заданий.

Так, например, с целью формирования основ регулятивных УУД, учащимся 5 класса можно предложить выполнить следующие задания в компьютерной среде «Живая математика» (рис. 1):

1. Составьте план действий для выполнения следующего задания: «Поле прямоугольной формы имеет площадь 56 а, его длина равна 80 м. Вычислите периметр поля и изобразите его план в чертеже».
2. Согласно составленному плану в задании 1, выполните задание: «Поле прямоугольной формы имеет площадь 56 а, его длина равна 80 м. Вычислите периметр поля и изобразите его план в чертеже».

Выполняя задания 1) и 2) обучающиеся работают в среде «Живая математика» – на рабочем поле оформляют план решения и осуществляют его реализацию.  Для проведения самопроверки и самоконтроля правильное выполнение заданий, с помощью специальных кнопок среды «Живая математика», можно скрыть от учащихся и показать только после их выполнения. Правильность итогового ответа можно проверить с помощью специальных инструментов «Живой математики», т.е. измерить искомый угол.

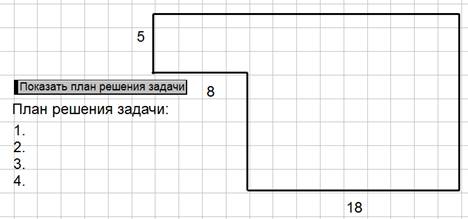
Рисунок. 1. Задание в компьютерной среде «Живая математика»

В ходе выполнения данного задания у учащихся формируются и отрабатываются не только предметные знания, но и универсальные учебные умения, такие как: правильно читать и понимать условие задания; составлять план решения; действовать в соответствии с планом; осуществлять самопроверку и самоконтроль.