Итоги разработки медицинской автоматизированной системы «Периметрия»

Аннотация. В статье рассматриваются вопросы автоматизации офтальмологического исследования полей зрения – периметрия. Нарушения при данном исследовании могут сигнализировать о наличии такого социально значимого заболевания как глаукома, а также дистрофии сетчатки, онкологического заболевания глаз и других. Прорисовка полей зрения занимает определённое время, а результат должен храниться в виде рисунка вместе с амбулаторной карточкой или историей болезни пациента.

Разрабатываемый программный продукт основан на математических алгоритмах построения кривых Безье, что позволяет эстетически сглаживать кривые между точками. Результат может сохраняться в стандартных графических форматах. Программа может применяться специалистами офтальмологического профиля, как автономно, так и интегрироваться в имеющуюся медицинскую информационную систему.

Аbstract. The article deals with the issues of automating the ophthalmological study of visual fields - perimetry. Violations in this study may signal the presence of such a socially significant disease as glaucoma, as well as retinal dystrophy, cancer of the eye and others. Drawing fields of view takes some time, and the result should be stored as a picture together with an outpatient card or a patient's history.

The software being developed is based on mathematical algorithms for constructing Bezier curves, which allows aesthetically smooth curves between points. The result can be saved in standard graphic formats. The program can be used by specialists of the ophthalmologic profile, both autonomously and integrated into the existing medical information system.

Ключевые слова: автоматизированная система, офтальмология, периметрия, автоматизация.

Keywords: automated system, ophthalmology, perimetry, automation.

Введение. На сегодняшний день офтальмологические заболевания влияют на качество жизни населения. Они могут приводить к частичной или полной потере зрения. Среди таких заболеваний можно выделить глаукому, при которой повышается внутриглазное давление [1]. Глаукома остается одной из основных причин слепоты и слабовидения и занимает ведущее место в нозологической структуре инвалидности [4]. Основными проявлениями данного заболевания являются изменения полей зрения, измерения которых фиксируются специальным исследованием – периметрия [2,6].

Периметрия на сегодняшний день помогает при диагностике таких офтальмологических заболеваний как глаукома, дистрофия сетчатки, ожоговое заболевание глаз, онкологические заболевания глаз, отслоение сетчатки, неврит или травма зрительного нерва [3]. Различают периметрию статическую и компьютерную. При статической периметрии используют специальный прибор периметр, во втором случае используют компьютер. И в том и в другом варианте результатом являются изображения полей зрения. Симптомами при данном исследовании являются сужение полей зрения различной степени и формы, выпадение полей зрения в виде скотом и другие.

Традиционно прорисовка полей зрения осуществляется вручную на основе специально напечатанных шаблонах, на которых специалисты ручкой или карандашом отмечают изменения или заштриховывают выпадение полей зрения. Такой способ содержит в себе определенные минусы. Данный листок может потеряться, стереться, испортиться. Намного удобнее было бы хранить данную информацию в электронном виде. Для осуществления прорисовки изменений полей зрения необходим специальный инструментарий, который бы позволил достаточно быстро отобразить часто встречающуюся патологию. Быстрая прорисовка должна основываться на математических принципах сглаживания кривых [5].

Целью работы является разработка медицинской автоматизированной системы «Периметрия».

Результаты. Основой в исследовании математических моделей для данного проекта, является интерполяция. Интерполяция (от лат. Inter-polis – “разглаженный, подновлённый, обновлённый; преобразованный”) – в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Основными способами интерполяции являются:

· Интерполяция методом ближайшего соседа;

· Интерполяция многочленами;

· Обратное интерполирование;

· Интерполяция функции нескольких переменных.

В данной работе был исследован способ интерполяции многочленами, так как в данном способе рассматривается вычисление многочленов в пространстве непрерывных функций. Данный способ широко используется в программировании и позволяет строить различные графики, основываясь на получении промежуточных результатов.

Существует следующие методы интерполяции многочленами:

· Линейная интерполяция;

· Сплайн-функция;

· Кубический сплайн;

· Интерполяционныймногочлен Лагранжа;

· Интерполяционные формулы Ньютона;

· Схема Эйткена;

·  Метод конечных разностей.

Самым простым и часто используемым методом, является линейная интерполяция. Она заключается в вычислении значений функции , для внутренних точек отрезка по известным значениям и . На рисунке 1 представлено графическое отображение линейной интерполяции.

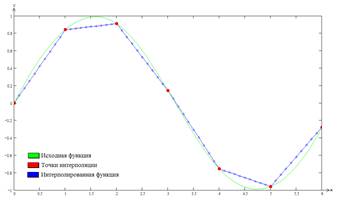
Рисунок 1. Применение линейной интерполяции

Сплайн-функция – это совокупность нескольких функций (кусочно заданная функция), где каждая из функций задана на каком-то множестве значений аргумента. Широко применяется в компьютерном моделировании.

Кубический сплайн (рисунок 2) – это функция , которая:

· На каждом отрезке является многочленом степени не выше третьей;

· Имеет непрерывные первую и вторую производные на всем отрезке ;

· В точках выполняется равенство , то есть сплайн интерполирует функцию в точках .

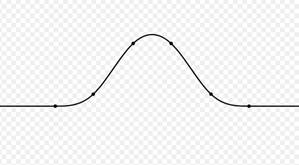
Рисунок 2. Кубический сплайн из семи сегментов

Интерполяционный многочлен Лагранжа, является многочленом минимальной степени, принимающим определенные значения в определенном наборе точек.

На рисунке 3 представлен пример, показывающий в применении интерполяционный многочлен Лагранжа для четырех точек и полиномов , каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных .

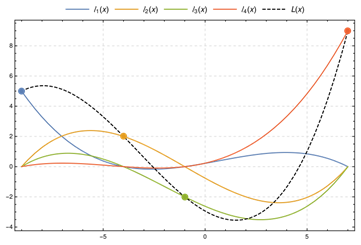
Рисунок 3. Интерполяционный многочлен Лагранжа и полиномы

Интерполяционные формулы Ньютона – это формулы в вычислительной математике, которые применяются для полиномиального интерполирования.

Схема Эйткена, является повторным способом вычисления многочлена Лагранжа, который позволяет за квадратичное время, относительно узлов интерполяции внедрять в данный многочлен новые точки.

Метод конечных разностей, является численным и позволяет решать дифференциальные уравнения, основанные на замене производных разностными схемами. Данный метод – сеточный.

Исходя из описанных выше методов интерполяции, самым подходящим является метод сплайн-функций, который широко используется в компьютерной графике. Далее мы исследуем алгоритмы кривых Безье, в составе которых используются сплайн-функции.

Кривые Безье, они же – Кривые Бернштейна – Безье были предложены Пьером Безье и Полем де Кастельжо, во второй половине XXвека (в 60-х годах). Пьер Безье и Поль де Кастельжо работали в автомобилестроении, где применяли данные кривые для построения кузовов автомобилей.

Кривые Бернштейна – Безье можно отнести к особому случаю многочленов Бернштейна, которые описал в 1912 году Сергей Натанович Бернштейн.

По определению Кривой Безье, является параметрическая кривая, которая задаются следующим выражением:

,

где:

· функция компонент для векторов опорных вершин;

·  – базисные функции кривой Безье – полиномы Бернштейна.

Полином Бернштейна задается выражением:

,

где:

·  – число сочетаний из по, где  – степень полинома, – порядковый номер опорной вершины.

Кривые Безье делятся на следующие виды:

· Линейные кривые;

· Квадратичные кривые;

· Кубические кривые;

· Кривые высших степеней.

Линейная кривая Безье, как видно из рисунка 4, представляет собой отрезок проходящий между двумя опорными точками.

Рисунок 4. Линейная кривая Безье

Данная кривая задается следующим выражением:

  ,

где и  – опорные точки, определяющие начало и конец отрезка.

Квадратичная кривая Безье (рисунок 5), в отличие от линейной задается тремяопорными точками и представляет собой сплайн и задается следующим выражением:

  ,

Прямые широко используются для описания символов, точнее их форм в шрифтах, а также для описания SWFфайлов, которые представляют проприетарный формат для векторной графики.

 ,  

,   

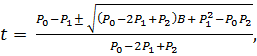
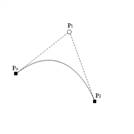
Рисунок 5. Квадратичная кривая Безье

Кубическая кривая Безье (рисунок 6), имеет четыре опорные точки, которые могут быть заданы как в 2- так и в 3-мерном пространстве тем самым определять форму кривой.

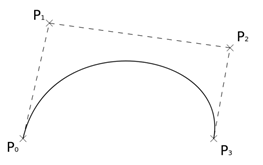
Рисунок 6. Кубическая кривая Безье

В параметрической форме кривая задается следующим выражением:

,    ,

где:

·  – точки через которые проходит кривая;

·  – точки, которые указывают направление кривой.

Так же кривая может записываться и в матричной форме:

,

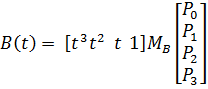где:

·  – базисная матрица Безье, заданная выражением:

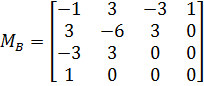
Весь исходный код написан в среде программирования Borland Delphi 7.

Интерфейс программы построен следующим образом, при запуске программы появляется окно, позволяющее пользователю создать новый или загрузить ранее сохраненный проект (рисунок 7), после чего он начинает работу в программе.

Рисунок 7. Окно выбора, при запуске в программу

Интерфейс главного окна программы состоит из шести групп компонентов (рисунок 8):

1. Главное меню программы;

2. Форм для ввода данных;

3. Блок с кнопками быстрого доступа;

4. Блок управления объектами;

5. Графический редактор;

6. Статус бар.

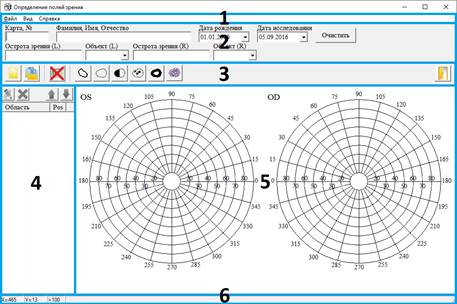
Рисунок 8. Интерфейс главного окна программы с разбивкой на группы

Главное меню программы состоит элементов, которые мы можем увидеть на рисунке 9.

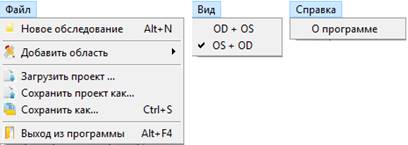
Рисунок 9. Развертка основных пунктов главного меню программы

Практически все элементы главного меню программы дублируется в блоке с кнопками быстрого доступа.

Формы ввода данных позволяют отобразить данные о пациенте и обследовании в графическом редакторе, пример мы можем увидеть на рисунке10.

Рисунок 10. Текст в графическом редакторе

Блок управления объектами позволяет управлять объектами, используя список объектов, а также отображает слои по порядку (рисунок 11).

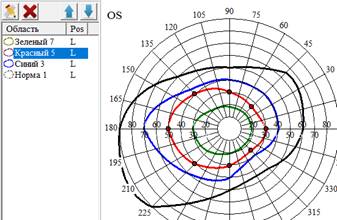
Рисунок 11. Блок управления объектами во время работы программы

Графический редактор позволяет манипулировать объектами с помощью мыши и имеет общее всплывающее меню (рисунок 12) с блоком управления объектами.

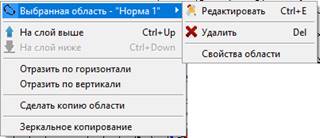
Рисунок 12. Всплывающее меню

Статус бар программы отображает три значения, где первые два являются положением курсора мыши в графическом редакторе, а третий показывает градусы поля зрения (OS или OD).

Так же в программе предусмотрена возможность редактирования объекта: изменение названия, границы и заливки (рисунок 13).

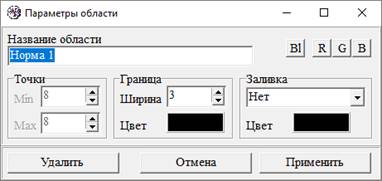
Рисунок 13. Редактирование свойств объекта

Хотелось бы отметить тот факт, что выше изложенное описание интерфейса является не совсем полным, так как тут не были показаны стандартные диалоговые окна Windows, так они нам повседневно встречаются в других Windows программах и не имеют отличия, этими окнами являются:

· окно сохранения файла;

· окно загрузки файла;

· окно вывоза запросов (сообщений) программы.

Выводы

Таким образом, была проведена работа по исследованию математических моделей программного построения непрямых линий, в основе которых лежит интерполяция. Рассмотрены основные способы данного метода, среди которых интерполяция методом ближайшего соседа, интерполяция многочленами, обратное интерполирование, интерполяция функции нескольких переменных. Исследован алгоритм построения кривых Безье, который позволяет по нескольким точкам рисовать сглаженную кривую линию. Данный алгоритм был положен в основу создания локальной автономной версии автоматизированной системы "Периметрия". Данная система позволяет в короткие сроки отобразить изменения полей зрения. При разработке данного продукта учитывались следующие функциональные составляющие: инициализация, графическая составляющая, управление объектами, общий функционал. Были запрограммированы основные процедуры и функции программы. При разработке интерфейса особое внимание уделялось наглядности и удобству использования функционалом. Интерфейс главного окна программы состоит из шести групп компонентов, позволяющий управлять построением изменений полей зрения. В целом разрабатываемый продукт позволит в значительной степени сократить время подготовки результатов периметрии и в дальнейшем хранить его в электронном виде.