Моделирование падения тела при наличии бокового ветра: построение математической модели

Моделирование как форма отражения действительности появляется в античную эпоху. Это время связано с возникновением научного познания. Не смотря на это, моделирование начинает широко использоваться лишь в эпоху Возрождения. Многие итальянские архитекторы и скульпторы использовали модели при проектировании своих сооружений. Моделирование широко применяется и в наши дни.

Моделирование – это процесс создания, исследования и практического использования моделей. Под моделью принято понимать объект любой природы, который в определенных условиях способен воспроизводить требуемые нам характеристики изучаемого процесса или явления.

Процесс моделирования состоит из нескольких этапов: содержательная постановка задачи, концептуальная постановка задачи, математическая постановка задачи.

Рассмотрим указанные этапы моделирования на примере задачи построения математической модели паления тела при наличии бокового ветра. Графическая иллюстрация рассматриваемой задачи представлена на рисунке 1.

Рисунок 1. Графическая иллюстрация изучаемого процесса

Содержательная постановка задачи – это модель изучаемого объекта или процесса, выраженная на каком-либо естественном языке. Например,  разработать математическую модель падения тела при наличии бокового ветра.

Концептуальная постановка задачи – это модель изучаемого объект или процесса, при формировании которой используются понятия и представления предметных областей знания, занимающихся изучением объекта модели.

Для нашей задачи концептуальная модель будет следующей: определить закон изменения координат центра масс тела при его падении под действием силы тяжести и наличии бокового ветра.

Для упрощения решения будущей модели необходимо ввести некоторые ограничения – гипотезы – перечень упрощений и пояснений относительно свойств и поведения объекта моделирования:

· движение происходит в поле силы тяжести с постоянным ускорением свободного падения g;

· сила сопротивления воздуха прямо пропорциональна скорости движения тела;

· динамика объекта моделирования описывается уравнениями классической механики Ньютона;

· эффектами, вызванными собственным вращением тела вокруг центра масс, можно пренебречь;

· сила ветра направлена перпендикулярно силе тяжести.

Для нахождения математических соотношений, описывающих рассматриваемый процесс, спроектируем уравнения второго закона Ньютона на оси неподвижной системы координат:

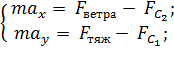
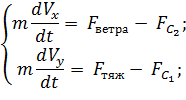
Дополним полученные уравнения известными из кинематики соотношениями между скоростями и координатами:

Начальные условия и ограничения будут иметь вид:

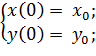
Таким образом, исходная задача свелась к решению задачи Коши для следующей системы уравнений:

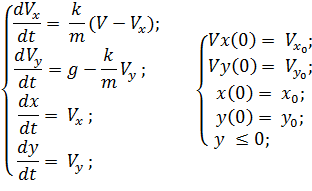
Перед решением данной модели и дальнейшим применением полученной математической модели для решения задач исследования или обучения, необходимо проверить ее на корректность, в противном случае, модель будет непригодной, так как получаемые результаты будут ошибочными. Для контроля правильности полученной модели необходимо провести следующие проверки:

· Контроль размерности;

· Контроль порядков;

· Контроль характера зависимостей;

· Контроль экстремальных ситуаций и особых точек;

· Контроль граничных условий;

· Контроль математической замкнутости.

Полученная математическая модель будет называться корректной, если для нее получен положительный результат всех контрольных проверок.

Выполнив проверки, можно убедиться, что полученная модель является корректной.

При этом у моделей имеются свои достоинства и недостатки.

К достоинствам можно отнести следующее:

· Снижение затрат на исследование или проектирование;

· Модели позволяют изучать опасные ситуации;

· Модели воспроизводят наиболее важные свойства объекта моделирования;

· Модели позволяют предсказывать новые свойства исследуемых объектов.

Среди достоинств модели имеют место быть и недостатки, такие как:

· Огрубление и упрощение описываемой реальности;

· Некорректная модель или некорректное использование модели, что приводит к получению формально верных, но фактически ошибочных результатов.