Исследование финитно-временного адаптивного метода фильтрации и прогнозирования навигационных параметров

В настоящее время повышение уровня безопасности полёта летательного аппарата является актуальной задачей. Для этого используются различные математические алгоритмы, в том числе и прогнозирующие, которые помимо авиации используются в различных областях.

В статье рассматриваются оптимальные алгоритмы дискретной фильтрации и прогноза навигационных параметров на примере оценки высоты полета летательного аппарата. Алгоритмы фильтрации и прогноза высоты полета летательного аппарат основываются на использовании финитно-временного метода оценки сигналов [1] и фильтрации Калмана в адаптивном и неадаптивном режимах работы. В качестве критериев оценки качества используются дисперсии ошибки оценки. В исследуемой системе для оценки навигационной координаты используется радиотехнический высотомер.

В работе рассматривается линейная модель измерения с аддитивной погрешностью. Моделями измеряемого сигнала  и погрешности  измерителя являются нормальные стационарные эргодические процессы некоррелированные между собой. На входе фильтра результат измерения определяется соотношением:

где i = 1…N, N – объём используемой выборки для прогноза сигналов,  – соответственно скалярные результаты измерения, полезного сигнала и погрешности измерения.

Как известно [1], использование финитно-временной обработки для фильтрации и прогнозирования сигналов значительно упрощает алгоритмы обработки сигналов. При этом позволяет применять единые алгоритмы обработки как в случае наличия коррелированных, так и некоррелированных погрешностей измерения, обеспечивает более устойчивую работу, повышает устойчивость работы алгоритмов относительно фильтрации Калмана.

Алгоритм прогнозирования сигналов на основе финитно-временного фильтра базируется на следствии теоремы ортогонального проецирования Пугачева [3] и в случае некоррелированности сигнала и помехи определяется следующей матрицей преобразования наблюдаемого сигнала:

где  – оптимальная по критерию среднего квадрата ошибки оценки матрица,  – матрица корреляционных моментов полезного сигнала,  – матрица корреляционных моментов результата измерения, d – дискрет. Размерности рассматриваемых матриц r×r, где r – память финитно-временного фильтра, pr – время прогноза сигнала на скользящем интервале времени.

Матрица корреляционных моментов измерений размерностью r×r равна:

Измеряемый сигнал  в случае дискретной обработки образуется в виде следующего вектора  размерностью r×1 за счет использования предыдущих результатов измерений к моменту времени i:

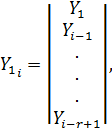
Оптимальная оценка прогноза сигнала определена по формуле:

В случае если интервал времени прогноза сигнала pr = 0, то  будет являться оценкой фильтрации сигнала в момент времени i.

Оценка точности фильтрации и прогноза на выбранный интервал времени для произвольного вида оценок финитно-временного метода прогнозирования равна:

где  – матрица корреляционных моментов оптимальных оценок, определяемая следующим выражением:

Оптимальная оценка точности фильтрации и прогноза после окончания переходного процесса также можно представить в следующем виде:

Статистическая оценка математического ожидания ошибки оценки определяется по формуле [4]:

где  – ошибка оптимальной оценки.

Статистическая оценка дисперсии ошибки оптимальной оценки  фильтрации и прогноза в случае наблюдаемых стационарных процессов вычисляется по следующему выражению:                                                                

Статистическая дисперсия  после окончания переходного процесса совпадает с теоретическими дисперсиями. Оценку времени адаптации финитно-временного алгоритма можно получить путем сравнения значений дисперсий и   при выбранном значении их разности.

Прогноз в случае априорной неопределенности матриц корреляционных моментов полезного сигнала  и погрешности  основывается на использовании байесова адаптивного метода оценки неизвестных матриц фильтрации и прогноза сигнала по результатам полученных измерений [6]. Для этой цели осуществляется статистическая оценка неизвестной  корреляционной матрицы результатов измерений  в соответствии с формулой:

где  – адаптивная оценка математического ожидания размерностью r×1, вычисленная по формуле:

В случае априорной неопределенности относительно корреляционной матрицы  и некоррелированности сигнала и помехи её оценка осуществляется в соответствии со следующей формулой:

В данном случае адаптивная оптимальная матрица оценки сигнала прогноза  вычислена по формуле:

В случае априорной неопределенности относительно корреляционной матрицы  и некоррелированности сигнала и помехи её оценка осуществляется в соответствии со следующей формулой:

В данном случае адаптивная оптимальная матрица оценки сигнала прогноза  вычислена по формуле:

Полученные статистические оценки указанных матриц 
 позволяют использовать приведенный выше алгоритм.

В случае если интервал времени прогноза сигнала pr = 0, то адаптивная оценка сигнала будет являться оценкой фильтрации сигнала.

Определение оптимальной оценки дискретного фильтра Калмана [5] осуществляется на основании теоремы Дуба [3], где оптимальный прогноз определяется условным математическим ожиданием:

где  – оптимальная оценка сигнала, X, Y – соответственно оцениваемый и наблюдаемый сигналы.

В качестве корреляционной характеристики оцениваемого сигнала выбирается следующая функция:

где i, j = 1…N, σ – среднеквадратическое отклонение от требуемого значения высоты полета, α – параметр корреляционной функции, d – дискрет.

Как известно, случайный нормальный процесс с данной корреляционной функцией является марковским процессом [2].

Моделью погрешности радиотехнического высотомера является белый шум, корреляционная функция которого определяется выражением:

где i, j = 1…N,  – среднеквадратическое отклонение белого шума,  – дельта-функция.

Анализ рассматриваемых алгоритмов фильтрации и прогноза сигнала в случае полной априорной неопределенности и адаптивной оценки матрицы корреляционных моментов полезного сигнала осуществлен в процессе моделирования при следующих исходных данных:

- объем выборки N = 5000;

- среднеквадратическое отклонение полезного сигнала ;

- среднеквадратическое отклонение погрешности радиовысотомера ;

- память финитно-временной обработки r = 5;

- интервал времени прогноза сигнала pr = 20;

- параметр корреляционной функции α = от 0,01 1/с:

- дискрет d = 5 с. Как известно, по теореме Котельникова дискрет не должен превышать значения:

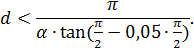
Сравнительные результаты моделирования для исследуемых алгоритмах приведены на следующих графиках:

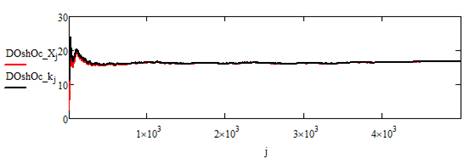
Рисунок 1. Изменение дисперсии ошибок оценок финитно-временной фильтрации на текущем интервале времени r·d (DOshOc_X) и фильтра Калмана (DOshOc_k) от дискретного времени i

Рисунок 2. Изменение дисперсии ошибок оценок финитно-временного прогноза на текущем интервале времени r·d (DOshOc_Xpr) и прогноза фильтра Калмана (DOshOc_kpr) от дискретного времени i

Рисунок 3. Изменение дисперсии ошибок оценок адаптивной финитно-временной фильтрации на текущем интервале времени r·d (DOshOc_Kx) и адаптивного прогноза фильтра Калмана (DOshOc_kA) от дискретного времени i

Рисунок 4 . Изменение дисперсии ошибок оценок адаптивного финитно-временного прогноза на текущем интервале времени r·d (DOshOc_Kxpr) и адаптивного прогноза фильтра Калмана (DOshOc_kApr) от дискретного времени i

Как видно из приведенных рисунков, финитно-временная обработка незначительно уступает по точности методу Калмана при выбранных исходных данных. При увеличении памяти финитно-временного алгоритма его точность прогноза будет приближаться к фильтрации Калмана. При этом адаптивная финитно-временная обработка по точности превосходит адаптивный прогноз Калмана.

По результатам проведенного моделирования была сделана сравнительная оценка методов обработки на робастность и помехозащищенность исследуемых алгоритмов. Диапазоны изменения данных: 

Рисунок 5. Изменение дисперсии ошибки оценки финитно-временного прогноза () и прогноза фильтра Калмана () от изменения параметра r

Рисунок 6.Изменение дисперсии ошибки оценки адаптивного финитно-временного прогноза () и адаптивного прогноза фильтра Калмана () от изменения параметра r

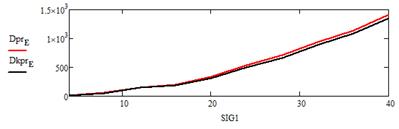
Рисунок 7. Изменение дисперсии ошибки оценки финитно-временного прогноза () и прогноза фильтра Калмана () от изменения параметра SIG1

Рисунок 8. Изменение дисперсии ошибки оценки адаптивного финитно-временного прогноза () и адаптивного прогноза фильтра Калмана () от изменения параметра SIG1

В результате проделанной работы было показано, что финитно-временная обработка при фильтрации и прогнозирования сигналов незначительно уступает по точности методу Калмана при выбранной памяти, но имеет более простой математический аппарат. Данные алгоритмы по свойствам робастности и помехозащищенности практически не отличаются друг от друга. При увеличении памяти финитно-временная обработка асимптотически стремится по точности к фильтрации Калмана, как в адаптивном режиме, так и при полной априорной неопределенности. Финитно-временная обработка является более универсальной по сравнению с фильтром Калмана.