Типичные ошибки школьников при решении дробно-рациональных неравенств на примере заданий из ЕГЭ

Перед тем, как анализировать типичные ошибки школьников при решении дробно-рациональных неравенств на примере заданий из ЕГЭ, дадим определение дробно-рациональному неравенству.

Определение 1. Дробно-рациональным неравенством называется неравенство вида , где P(x), Q(x) – многочлены.

Примечание: Дробно-рациональное неравенство может быть записано и в другом виде, как  или  или 

Типичные ошибки, допускаемые школьниками при решении дробно-рациональных неравенств рассмотрим на конкретных примерах из ЕГЭ-2019

1)             [1, c.18]

Правильным решением неравенства будет следующее решение: исходное неравенство равносильно неравенству

. Данное неравенство решается методом интервалов. Верное решение данного неравенства представлено на рис.1.

Рис. 1. Верное решение неравенства 

В процессе решения данного неравенства могут быть допущены следующие ошибки:

- корни многочленов неправильно нанесены на ось (см. на рис. 2)

Рис. 2. Ошибки в решении дробно-рационального неравенства: обе точки нанесены как выколотые

- сокращены переменные х (грубая ошибка). В результате чего школьник придет к уравнению , решением которого будут все действительные числа.

- школьник может посчитать, что решение данного неравенства сводится к решению 2-х линейных неравенств, составляющих систему, т.е.

- школьник может предположить, что для решения данного неравенства следует решить неравенство

и при этом нанести на ось выколотый корень уравнения х=0. То есть, в результате данной ошибки получим следующее решение:

.

Окончательно, ученик придет к тому, что

2)    [1, c.38]

Правильным решением данного дробно-рационального неравенства является его преобразование к неравенству

.

Это неравенство является квадратным и решается методом интервалов. На ось наносится выколотый кратный корень x=3

Решением неравенства будут все числа, кроме х=3 или совокупность интервалов (-∞; 3) U (3; +∞)

В процессе решения данного неравенства могут быть допущены следующие ошибки:

- ученик может свести данное неравенство к следующему неравенству

.

То есть в данном случае, школьник потерял кратный корень, превратив исходное квадратное неравенство в линейное.

- ученик неправильно раскрыть формулу сокращенного умножения, в результате чего придет к следующему неравенству

.

Затем на оси будут нанесены корни х=3 и х=-3. В итоге, школьник придет к тому, что решением неравенства может быть интервал (-3;3) или совокупность интервалов (-∞; -3) U (3; +∞)

3) 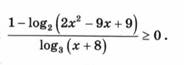      [1, c.76]

Рассмотрим правильное решение неравенства. Так как дробь неотрицательна, то необходимо рассмотреть два случая

1 случай:

2 случай:

Учтем, что между данными случаями необходимо поставить или, т.е. рассмотренные системы неравенств объединить в совокупность.

Рассмотрим решение 1 случая.

Рассмотрим решение двух неравенств системы раздельно.

                      (1)

Решение данного неравенства равносильно решению системе неравенств:

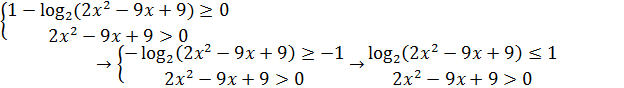
Решим каждое из неравенств системы отдельно:

D=81-56=25

x1= (9-5)/4=1;

x2=(9+5)/4=14/4=7/2=3,5

Решением неравенства  будет интервал 

Теперь решим неравенство 

D=81-72=9

x1= (9-3)/4=6/4=3/2;

x2=(9+3)/4=12/4=3

Решением неравенства  будет совокупность интервалов 

Окончательным же решением исходного неравенства будет пересечение найденных областей: 

Рассмотрим решение неравенства (2) 1 случая.

Решение неравенства эквивалентно системе неравенств:

Решением же системы 1 случая является пересечение найденных решений неравенств (1) и (2), а именно пересечение промежутков  и . Окончательным решением системы 1 случая является промежуток 

Рассмотрим решение системы 2 случая

Рассмотрим решение двух неравенств системы раздельно.

Решение данного неравенства равносильно решению системе неравенств:

Решим каждое из неравенств системы отдельно:

D=81-56=25

x1= (9-5)/4=1;

x2=(9+5)/4=14/4=7/2=3,5

Решением неравенства  будет интервал 

Теперь решим неравенство 

D=81-72=9

x1= (9-3)/4=6/4=3/2;

x2=(9+3)/4=12/4=3

Решением неравенства  будет совокупность интервалов 

Окончательным же решением неравенства  будет пересечение найденных областей: . Таким образом, решением неравенства  будет промежуток 

Рассмотрим решение второго неравенства 2 случая.

Решение неравенства эквивалентно системе неравенств:

Решением же системы 2 случая является пересечение найденных решений неравенств, а именно пересечение промежутков  и . Окончательным решением системы 2 случая является промежуток .

Решением же исходного неравенства является объединение решений 1 и 2 случая, т.е. объединение промежутков .

Рассмотрим типичные ошибки школьников при решении данного неравенства:

- Данное неравенство школьник может свести к неравенству

,

выколов на оси точку х=8.

Далее ученик придет к такому неравенству

,

которое он правильно преобразует, т.е.

- Искомое неравенство школьник может свести к системе неравенств  (1)

Далее каждое из неравенств системы школьником могут решаться отдельно и при этом первое неравенство ученик может неправильно преобразовать, например,

 и т.д.

- Искомое неравенство школьник может свести к следующему неравенству

() 

Данное неравенство может быть сведено к системе неравенств (1).

Затем первое неравенство системы (1) школьник преобразует, как

Второе неравенство системы

школьник преобразует, как

То есть в результате система

будет преобразована к системе

В этом случае, ошибка состоит в том, что ученик не учел, что подлогарифмируемые выражения должны быть положительны, т.е. неравенство

должно быть преобразовано в систему неравенств 

А неравенство

должно быть также преобразовано к системе неравенств,

Помимо рассмотренных ошибок в решении данного неравенства, ошибки могут возникнуть в расчетах, в неправильном переносе слагаемых из одной части в другую, в не изменении знака неравенства в случае его умножения на -1.

Вывод

Итак, при решении школьниками дробно-рациональных неравенств на ЕГЭ ими допускаются следующие основные ошибки:

- ошибки в вычислениях;

- ошибки в преобразованиях (неравенство преобразовано не к равносильному неравенству или системе неравенств, не изменены знаки слагаемых при их переносе из одной части в другую, не изменен знак неравенства при умножении всего неравенства на отрицательное число);

- незнание свойств логарифмической и показательной функции, неумение решать квадратные уравнения и неравенства;

- неправильно сокращены слагаемые;

- неправильно нанесены точки на ось (например, точка должна быть выколотой, а она изображается, как закрашенная).

Для предупреждения ошибок при решении дробно-рациональных неравенств во время подготовки к ЕГЭ рекомендуется: выполнять самопроверку, взаимопроверку решений, выполнять такие задания, как написать правильное решение и решение с ошибкой, проанализировав последнее.