Модели и методы решения задачи маршрутизации для эвакуации людей с ограниченными возможностями во время чрезвычайных ситуации
Журнал: Научный журнал «Студенческий форум» выпуск №22(73)
Рубрика: Технические науки

Научный журнал «Студенческий форум» выпуск №22(73)
Модели и методы решения задачи маршрутизации для эвакуации людей с ограниченными возможностями во время чрезвычайных ситуации
Аннотация. Данная статья посвящена моделям и методам решения задачи маршрутизации для эвакуации людей с ограниченными возможностями. Изложены и обоснованы основные понятия и возможности решения задачи маршрутизации с помощью генетического алгоритма. Описываются методы и алгоритмы решения задачи.
Abstract. This article is devoted to models and methods for solving the problem of routing for the evacuation of people with disabilities. The basic concepts and possibilities of solving a routing problem using a genetic algorithm are stated and justified. The methods and algorithms for solving the problem are described.
Ключевые слова: задача о маршрутизации, задача о коммивояжера, генетический алгоритм, Гамильтонов цикл, эвакуация людей с ограниченными возможностями.
Keywords: routing problem, traveling salesman problem, genetic algorithm, Hamiltonian cycle, evacuation of people with disabilities.
По статистическим данным в Казахстане насчитывается 674,2 тыс. инвалидов. Причем 16 % из их числа – инвалиды I группы и 35,5 % инвалиды II группы.
Опрос людей с ограничениями зрения в России показал, что при движении в нормальных условиях от 2 % (движение в здании) до 8 % (движение по улицам города) слепых и слабовидящих людей могут передвигаться только с сопровождающим. В случае необходимости движения по незнакомому пути количество людей, которым необходим проводник, возрастает в несколько раз. По этой причине, люди с ограниченными возможностями нуждаются в помощи при эвакуации из зоны чрезвычайной ситуации. В условиях чрезвычайных ситуации, каждая сэкономленная минута может означать несколько спасенных жизней. И оптимизация маршрута может помочь сэкономить время для спасения большего количества жизней.
Для решения данной проблемы, были поставлены следующие задачи:
1) Рассмотреть основные характеристики концептуальных подходов и методов решения задачи маршрутизации для эвакуации людей с ограниченными возможностями
2) Разобрать методы решения задачи и привести практические примеры.
3) Сделать выводы о практическом применении решения задачи маршрутизации для эвакуации людей с ограниченными возможностями.
Маршрут – это последовательность (цепочка) отрезков соединяющихся узлов между собой, где первый и последней узел в этой цепочке совпадают. Узлами являются адреса людей с ограниченными возможностями.
Координаты узлов определяется по адресам задаваемые в виде текста в базе данных, например, ул. Сейфуллина, дом 130, кв. 17 или микрорайон 3, д.14, кв. 30.
Эти адреса наносятся на карту города, которые затем программным методом из библиотеки Java переводятся в Декартовые координаты.
Пример построения маршрутов для эвакуации в зоне чрезвычайной ситуации показан на рисунках 1, 2 и 3.

Рисунок 1. Построенный Гамильтонов цикл в зоне чрезвычайной ситуации

Рисунок 2. Разделение эвакуируемых людей по транспорту в зависимости от вместимости

Рисунок 3 – Сформированные маршруты для эвакуации в зоне чрезвычайной ситуации
Маршрут может определяться с разным уровнем полноты:
1 уровень – определение последовательности нахождения адреса людей с ограниченными возможностями относительно таксопарка по схеме траектории маршрута.
2 уровень – к тем данным, что на первом уровне полноты определения маршрута еще добавятся данные о расстоянии между адресами людей с ограниченными возможностями по схеме траектории маршрута.
3 уровень – к тем данным, что на первом уровне полноты определения маршрута еще добавится данные о качестве улиц маршрута и проходимость пути.
Здесь формулируем задачу построения маршрута, решением которой является такая цепочка последовательности узлов, для которой суммарное расстояние или стоимость между узлами минимальна.
Постановка задачи коммивояжера:
![]() (1)
(1)
![]()
![]()
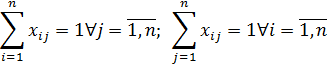
Аналогично формулируется задачи маршрутизации, коммивояжера и построение Гамильтонова цикла, т.е. все эти задачи является схожими задачами и имеют идентичную формулировку.
Данная задача может быть решена множеством методов, в частности следующими:
Метод ветвей и границ.
Метод локальных улучшений.
Приближенные и эвристические методы.
Псевдополиномиальные алгоритмы.
Метод случайного поиска.
Содержание задачи спасение людей с ограниченными возможностями в условиях чрезвычайных ситуации сводится к перевозке людей с ограниченными возможностями в транспорте с ограниченной вместимостью и отправкой их на N пунктов за пределами зоны эвакуаций.
Другая формулировка задачи построения маршрута или задачи коммивояжера сводится к задаче на графе, который построен предварительно, и она формулируется таким образом.
Дан полный взвешенный граф из N вершин, необходимо найти Гамильтонов цикл, имеющий минимальный вес. Или математически (2), где N – количество вершин графа, сij – вес ребра, ведущего из вершины i в вершину j.
![]() (2)
(2)
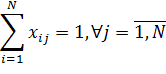
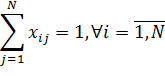
![]()
С целью решения задач на оптимизацию из комбинаторики, а именно такой и является задача, заданная выше, которая при этом использует в себе специфичные алгоритмы, несколько главных можно выделить среди них, а именно:
1) Метод отсечения.
2) На комбинаторику
3) На приближенное значение.
ГА, генетические алгоритмы, имеют свое отношение к 3 типу.
Но, генетические алгоритмы не имеют свойство применяться в чистом вид, такие алгоритмы основываются на специфике поставленных задач и другой эвристики локального улучшения в форме жадных алгоритмов. Все две, подлежащие рассмотрению в работе задачи имеют ограничения и соответственно являются задачами с ограничениями. С целью успешного решения поставленных вопросов при помощи генетического алгоритма, мы обязаны использовать методы избавления от этих ограничений. Такие методы имеют разделение на 3 формы: отображающие, непрямые, прямые.
Одним из основных способов ухода от ограничений к задаче коммивояжера есть декодеры, именно они имеют отношение к методам, которые отображают ограничения, а также методы, которые дают гарантии к допустимости решения. Декодер имеет свойство модифицировать пространство поиска так, что способен гарантировать получение допустимого решения, при этом устанавливая соответствие среди области допустимых решений, а также их представлениями. Если же к задаче о ранце может применяться классическая бинарная форма, то с целью решения задачи коммивояжера оно не станет естественным.
Более же естественными представлениями станут перестановки из номеров вершин графа с целью кодировки допустимого Гамильтонова алгоритма. В таком случае число в плане представления имеет значение номера вершины, а вершины же в свою очередь имеют проявление в соответствии с порядком обхода. Сама же идея состоит в следующем, а именно: первым делом сформировывается эталонный список вершин, затем к каждой соотносится свой порядковый номер в эталонном списке. Вершины имеют свойство кодироваться в порядке появления их же в обходе, далее, уже закодированные вершины исключаются из списка, а порядковые номера оставшихся вершин соответственно изменяются. В таком процессе мы наблюдаем взаимно-однозначное соответствие среди решения, а также представления.
Примером метода, которое гарантирует допустимость решения, является использование операторов, а именно: перестановочного представления и специальных генетических операторов. Именно примером декодера является использование в процессе позиционного представления.
Далее представим схему алгоритма генетики.
Именно следующий вид имеет схема генетического алгоритма в его классическом варианте.
1) Инициация изначального момента времени t=0. Рандом-образом сформировывается начальная популяция, которая в свою очередь состоит из k особей. B0={A1, A2,…, Ak}.
2) Далее вычисляется индивидуальная приспособленность каждой особи FAi =fit(Ai ), i=1…k, а также популяции в общем Ft =fit(Bt ) (иногда называемое понятием фиттнес). Вычисление данной функции определяет степень того, на сколько подходит особь, которая была описана данной хромосомой с целью решения задачи.
3) После этого следует выбор особей Ac, находящихся в популяции Ac =Get(Bt )
4) С определенной вероятностью (вероятностью кроссовера Pc) выбрать вторую особь из популяции Ac1 =Get(Bt) и произвести оператор кроссовера Ac =Crossing(Ac, Ac1 ).
5) С определенной вероятностью (вероятностью мутации Pm) выполнить оператор мутации Ac =mutation(Ac).
6) С определенной вероятностью (вероятностью инверсии Pi) выполнить оператор инверсии Ac =inversion(Ac).
7) Поместить полученную хромосому в новую популяцию insert(Bt+1, Ac).
8) Выполнить операции, начиная с пункта 3, k раз.
9) Увеличить номер текущей эпохи t=t+1.
10) Если выполнилось условие останова, то завершить работу, иначе переход на шаг 2.
Далее мы раскроем частные этапы алгоритма в кратком варианте.
Особо-большую степень в успешной работе алгоритма имеет этап отбора родительских хромосом на шаге под номером 3, а также под номером 4. Наряду с этим, возможны различные варианты. Метод отбора рулеткой имеет свойство использоваться наиболее часто. Во время пользования данным методом, вероятность по выбору хромосомы имеет определение по ее приспособленности, в формульном виде: PGet(Ai) Fit(Ai)/Fit(Bt). В свою очередь, использование данного метода имеет свойство приводить к тому, что вероятность по передаче признаков к более приспособленным единицам возрастает. Следующий же часто-используемый алгоритм является турнирный отбор. Его смысл заключается в том, что происходит случайный выбор нескольких особей среди всей популяции (чаще всего 2), а победителем же в свою очередь определяется особь, имеющая наибольшую приспособленность. При этом, в различных реализациях алгоритмической работы имеет место применение, так называемая стратегия элитизма, которая имеет смысл в том, что особи, имеющие большую приспособленность с гарантией переходят в новую популяцию. Использование элитизма обычно позволяет ускорить сходимость генетического алгоритма. Недостаток использования стратегии элитизма в том, что повышается вероятность попадания алгоритма в локальный минимум.
Другой важный момент – определение критериев останова. Обычно в качестве них применяются или ограничение на максимальное число эпох функционирования алгоритма, или определение его сходимости, обычно путем сравнивания приспособленности популяции на нескольких эпохах и остановки при стабилизации этого параметра.
В виде блок схемы простой генетический алгоритм можно представить в виде как на рисунке 2.
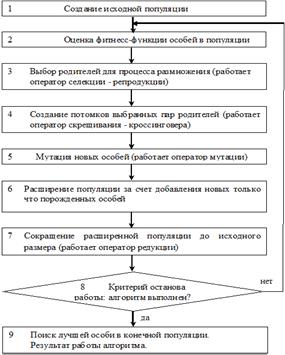
Рисунок 4. Блок-схема простого генетического алгоритма
Приведем вариант постановки задачи построения маршрута для решения генетическим алгоритмом таким образом. Дан граф ![]() , где
, где ![]() - множество вершин графа (адреса доставки товаров),
- множество вершин графа (адреса доставки товаров), ![]() - множество ребер (возможные пути между адресами). Дана матрица чисел
- множество ребер (возможные пути между адресами). Дана матрица чисел ![]() , представляющих собой стоимость переезда из вершины
, представляющих собой стоимость переезда из вершины ![]() .Требуется найти перестановку
.Требуется найти перестановку ![]() из элементов множества
из элементов множества ![]() такую, что значение целевой функции равно
такую, что значение целевой функции равно
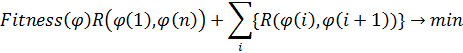
Для неполного графа дополнительным ограничением на величину ![]() являются:
являются:
![]()
Решение этой задачи генетическим алгоритмом состоит из следующих этапов.
Генерация первоначальной популяции. Размер популяции, необходимой для решения задачи составляет ![]() , где
, где ![]() - количество вершин в графе. При создании хромосомам предъявляется единственное требование: каждый узел должен встречаться в последовательности не более одного раза, и каждый из узлов должен входить в эту последовательность. Для обеспечения выполнения заданных условий используется структура SortedSet<Int32>, доступная пользователям платформы Microsoft.net Framework. Контроль за реальным существованием сгенерированного пути в графе не важен, так как нежизнеспособные особи будут преобразованы и устранены в ходе выполнения алгоритма.
- количество вершин в графе. При создании хромосомам предъявляется единственное требование: каждый узел должен встречаться в последовательности не более одного раза, и каждый из узлов должен входить в эту последовательность. Для обеспечения выполнения заданных условий используется структура SortedSet<Int32>, доступная пользователям платформы Microsoft.net Framework. Контроль за реальным существованием сгенерированного пути в графе не важен, так как нежизнеспособные особи будут преобразованы и устранены в ходе выполнения алгоритма.
Кроссинговер. Для решения поставленной задачи был реализован "жадный" алгоритм кроссинговера - поиск локальных оптимумов и добавление соответствующих узлов в возможный маршрут коммивояжера.
"Жадный" алгоритм кроссинговера:
1) Для каждой пары родительских хромосом случайным образом выберем тоску кроссинговера и в качестве номера стартовой вершины в графе возьмем номер отмеченного гена в хромосоме.
2) Сравним частичную стоимость путей, ведущих из текущих вершин в хромосомах-родителях, и выберем из них кратчайший.
3) Если выбранная таким образом вершина графа уже была включена в частичный путь, то нужно взять случайную вершину из числа еще не отмеченных. Присвоить полученной таким образом вершине значение текущей.
4) При преждевременном образовании цикла выбирается другой кратчайший путь.
5) Повторяем шаги 2 и 3 до тех пор, пока не будет построен путь, который может быть предполагаемым гамильтоновым циклом.
6) Конец работы алгоритма.
Селекция. Именно путем элитного отбора происходит селекция особей в популяции, а именно: в качестве особей следующих поколений отбираются 50 процентов более приспособленных, то есть имеющих Гамильтоновых цикл наименьшей длины. Сам же процесс по отбору имеет смысл только тогда, когда в популяции имеются особи, которые отличаются друг от друга, именно поэтому в качестве точки останова взято полное отсутствие разнообразия в поколении, то есть именно тот момент, при котором все особи в популяции являются одинаковыми. Данный выбор обуславливается тем, что отсутствие разнообразия дает понять, что для настоящих данных, а также условий стал достигнут глобальный оптимум (на самом деле который способен оказаться только лишь локальным оптимумом, наиболее ближайшим к глобальному), а дальнейшее же произведение алгоритма не способно привести к появлению новых оптимальных сочетаний узлов. Если в графе отсутствует Гамильтонов цикл, то алгоритм завершится через ![]() шагов. На рисунке 3 описана блок-схема общего хода алгоритма, а также взаимодействие всех вышеуказанных операторов. Следует отметить, что данная программа не всегда предоставляет точный результат, что в свою очередь обусловлено тем, что генетические алгоритмы являются алгоритмами с целью приближенного вычисления. Практика показывает, что пользователь может получить верный ответ примерно в 92% случаев. Временная сложность данного алгоритма составляет
шагов. На рисунке 3 описана блок-схема общего хода алгоритма, а также взаимодействие всех вышеуказанных операторов. Следует отметить, что данная программа не всегда предоставляет точный результат, что в свою очередь обусловлено тем, что генетические алгоритмы являются алгоритмами с целью приближенного вычисления. Практика показывает, что пользователь может получить верный ответ примерно в 92% случаев. Временная сложность данного алгоритма составляет ![]() . В лучшем случае временная сложность алгоритма составляет
. В лучшем случае временная сложность алгоритма составляет ![]() .
.
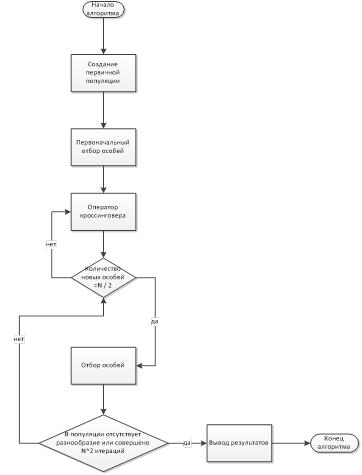
Рисунок 5. Блок-схема общей схемы алгоритма и взаимодействие всех операторов генетического алгоритма
Приведем пример вычисления или определения оптимального маршрута.
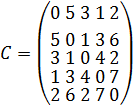
Оптимальный маршрут выглядит так: ![]()
Пройденное коммивояжером расстояние равно 9.
Все возможные маршруты выписаны в таблицу 1:
Таблица 4.
Возможные маршруты для прохождения пути коммивояжера
|
Маршрут |
Стоимость |
|
|
19 |
|
|
16 |
|
|
16 |
|
|
20 |
|
|
18 |
|
|
25 |
|
|
16 |
|
|
18 |
|
|
18 |
|
|
15 |
|
|
9 |
|
|
14 |
Жирным шрифтом выделен маршрут с наименьшей стоимостью.
Заключение: в ходе написания данной статьи было разобрано множество моделей и методов решений задачи для планирования маршрутизации с целью эвакуации людей с ограниченными возможностями. Дано полное изложение, а также обоснование фундаментальных понятий наряду с возможностями решения задачи маршрутизации, с использованием генетических алгоритмов. Дано описание методов, а также алгоритмов решения задачи.
С целью решения поставленной проблемы был решен ряд основных задачи, а именно: рассмотрены главные характеристики концептуальных подходов и методов решения задачи маршрутизации с целью эвакуации людей с ограниченными возможностями, разобраны методы решения задачи и приведены практические примеры, выполнены выводы о практическом применении решения задачи маршрутизации с целью эвакуации людей с ограниченными возможностями.
Полностью раскрыты и обоснованы схемы и реализация каждого из алгоритмов, обозначенных в работе. Построены модели, а также методы решения задачи маршрутизации для эвакуации людей с ограниченными возможностями во время чрезвычайных ситуации.

