Оценка качества моделирования исходных графиков электрических нагрузок распределительных сетей
Журнал: Научный журнал «Студенческий форум» выпуск №22(73)
Рубрика: Технические науки

Научный журнал «Студенческий форум» выпуск №22(73)
Оценка качества моделирования исходных графиков электрических нагрузок распределительных сетей
В статье приводятся обоснования использования обобщённых (ортогональных) графиков электрических нагрузок (ОГН), полученных на факторном пространстве признаков методом главных компонент [1–3] по данным статистически представительной выборки графиков нагрузок узлов районной электроэнергетической системы, для моделирования нагрузок, не входящих в указанную совокупность.
Получение ОГН и их свойства. Для матрицы корреляционных моментов (МКМ) центрированных значений мощностей вычисляются М собственных векторов в порядке убывания модулей собственных значений. Решение проблемы собственных значений выполнено для реальной статистически представительной совокупности суточных графиков нагрузки (объём от 48 до 100) в компьютерных программных комплексах (MATLAB, MATHEMATICA и др.), в частности с использованием эффективного итерационного метода, позволяющего получить устойчивый результат с контролируемой точностью. В результате отыскиваются значения первопричин – факторов, отражающих имеющуюся связь между исходными признаками – анализируемыми графиками нагрузок и соответствующими собственными векторами МКМ, малое количество которых используется в дальнейшем вместо признаков. Каждому из собственных векторов соответствует фактор – ОГН, являющийся линейной комбинацией исходных графиков ![]()
![]() , центрированных относительно своих математических ожиданий MPi,, MQi
, центрированных относительно своих математических ожиданий MPi,, MQi
|
|
(1) |
где ![]() ,
, ![]() – компоненты собственного вектора
– компоненты собственного вектора ![]() 2n-мерной МКМ;
2n-мерной МКМ;
Также как и собственные векторы, ОГН являются ортогональными (статистически независимыми), некоррелированными (несвязанными) статистическими величинами, отражающие общие закономерности, основные свойства изменения конфигурации электрических нагрузок. Выделенные факторные модели обладают свойством универсальности придают моделям, статистическому методу и в целом процессу моделирования множества режимов (многорежимности) свойства линейности и аддитивности и позволяют с достаточной точностью восстановить исходные параметры изменения нагрузок на интервале времени. В качестве примера на рисунке представлены ОГН, соответствующие первым трём максимальным собственным числам и собственным векторам МКМ, полученной для совокупности 48 исходных суточных графиков одной из энергосистем [4]. Первые три ОГН отражают около 80 % полной дисперсии исходных графиков нагрузок.
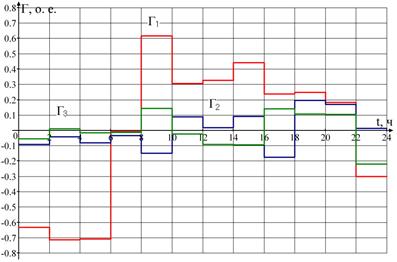
Рисунок 1. Суточные ОГН с количеством интервалов постоянства d = 12
Восстановление исходных графиков нагрузки с помощью ОГН. Метод является эффективным, поскольку обратные преобразования в признаковое пространство позволяют использовать небольшое число М<< 2n главных факторов – ОГН с целью моделирования исходных изменений нагрузок. В этом случае исходные графики Pi, Qi восстанавливаются с помощью известных математических ожиданий MPi,, MQi и моделируемых отклонений от математических ожиданий в виде линейной комбинации двух-четырёх ОГН:
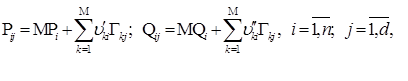 (2)
(2)
где d – количество интервалов осреднения суточного графика нагрузки.
Анализ результатов экспериментальной выборки. Для выборки из 8 схем распределительной сети напряжением 35, 110 кВ с количеством узлов от 2-х до 4-х с электропотреблением, заданным графиками активных и реактивных нагрузок предприятий различных отраслей промышленности [5] составлены МКМ, для которых получены ОГН, соответствующие первым двум собственным векторам. С помощью ОГН восстановлены исходные графики нагрузок и выполнен расчёт потерь ЭЭ в рассматриваемых сетях. Результаты расчёта и сопоставительный анализ качества моделирования представлен далее.
Используемая выборка характеризуется значительной неравномерностью KНР и малой плотностью (заполненностью) KЗ графиков нагрузок (табл. 1). Произведён расчёт средней относительной ошибки
Предоставлена доля вклада при учёте М первыми ОГН
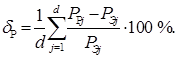 (3)
(3)
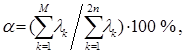 (4)
(4)
где λk – собственное число.
Также для анализа используется коэффициент корреляции
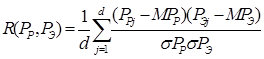 (5)
(5)
Таблица 1
Оценка качества моделирования графиков
|
№ схемы |
№ узла |
α, % |
KЗ |
KНР |
R |
|
|
|
1 |
1 |
93,5 |
0,757 |
0,604 |
0,999 |
0,63 |
99,37 |
|
2 |
0,790 |
0,619 |
0,990 |
2,00 |
98,00 |
||
|
2 |
1 |
97,9 |
0,801 |
0,618 |
0,653 |
4,29 |
95,71 |
|
2 |
0,822 |
0,552 |
0,991 |
1,81 |
98,19 |
||
|
3 |
1 |
89,7 |
0,800 |
0,700 |
0,998 |
0,74 |
99,26 |
|
2 |
0,839 |
0,712 |
0,461 |
7,00 |
91,00 |
||
|
3 |
0,662 |
0,515 |
0,998 |
2,37 |
87,63 |
||
|
4 |
0,882 |
0,745 |
0,657 |
6,15 |
93,85 |
||
|
4 |
1 |
95,8 |
0,833 |
0,667 |
0,999 |
0,26 |
99,74 |
|
2 |
0,844 |
0,641 |
0,871 |
5,92 |
94,08 |
||
|
3 |
0,832 |
0,680 |
0,762 |
5,54 |
94,46 |
||
|
4 |
0,887 |
0,805 |
0,884 |
3,02 |
96,98 |
||
|
5 |
1 |
93,6 |
0,841 |
0,741 |
0,986 |
1,18 |
98,82 |
|
2 |
0,806 |
0,697 |
0,939 |
3,15 |
96,85 |
||
|
3 |
0,840 |
0,750 |
0,702 |
6,32 |
93,68 |
||
|
4 |
0,833 |
0,689 |
0,983 |
1,90 |
98,10 |
||
|
6 |
1 |
85,6 |
0,850 |
0,741 |
0,841 |
4,18 |
95,82 |
|
2 |
0,730 |
0,378 |
0,922 |
7,24 |
90,76 |
||
|
3 |
0,724 |
0,509 |
0,980 |
3,42 |
96,58 |
||
|
4 |
0,688 |
0,361 |
0,950 |
5,65 |
94,35 |
||
|
7 |
1 |
84,0 |
0,757 |
0,604 |
0,944 |
3,96 |
96,04 |
|
2 |
0,801 |
0,618 |
0,936 |
4,25 |
95,75 |
||
|
3 |
0,841 |
0,741 |
0,772 |
4,76 |
95,24 |
||
|
4 |
0,730 |
0,378 |
0,977 |
3,72 |
96,28 |
||
|
8 |
1 |
82,3 |
0,790 |
0,619 |
0,982 |
2,36 |
97,64 |
|
2 |
0,822 |
0,552 |
0,916 |
6,18 |
93,82 |
||
|
3 |
0,805 |
0,697 |
0,728 |
7,27 |
92,73 |
||
|
4 |
0,724 |
0,503 |
0,999 |
0,83 |
99,17 |
||
|
Среднее значение точности восстановления ГЭН |
95,7 |
||||||
Из результатов расчёта (табл.1) следует, что использование двух собственных значений и соответствующих собственных векторов отражает от 82 до 92 % исходных МКМ. Полученные из МКМ первые два ОГН применительно к каждой схеме моделируют (восстанавливают) исходные графики нагрузок с относительной ошибкой от 0,63 до 7,3%, отражая до 95,7 % полной дисперсии исходных нагрузок с корреляционной связью в интервале 0,65-- 0,99 расчётных и эталонных (исходных) параметров.
Расчёт потерь электрической энергии по восстановленным графикам нагрузки. Также для сопоставления с предыдущими расчётами в данной выборке схем выполнено моделирование графиков нагрузок с помощью трёх обобщённых ОГН (рис. 1), представленных в таблице 2 [4]. Графики электрических нагрузок, исследуемые в данной работе, не входили в обучающую выборку, из которой получены обобщённые ОГН.
Таблица 2.
Суточные типовые обобщённые графики нагрузок
|
Номера графиков |
Временной промежуток, час |
|||||||||||
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
|
|
1 |
-0,633 |
-0,714 |
-0,709 |
-0,0073 |
0,618 |
0,306 |
0,327 |
0,441 |
0,238 |
0,248 |
0,182 |
-0,300 |
|
2 |
-0,0928 |
-0,0423 |
-0,0815 |
-0,0345 |
-0,149 |
0,0886 |
0,0192 |
0,0907 |
-0,176 |
0,196 |
0,170 |
0,018 |
|
3 |
-0,0556 |
-0,0097 |
0,0154 |
-0,0118 |
0,143 |
-0,0233 |
-0,0922 |
-0,0937 |
0,141 |
0,108 |
0,105 |
-0,219 |
Выполнено сопоставление точности вычисления статистическим методом [1,2,6] потерь ЭЭ (∆Э2) при моделировании графиков нагрузок данной выборки схем двумя первыми ортогональными графиками каждой схем и потерь ЭЭ (ΔЭО,) при моделировании изменения нагрузок тремя обобщёнными ОГН (табл.2).
Данные расчётные значения потерь ЭЭ сопоставлены с эталонными, в качестве которых приняты потери ЭЭ, полученные непосредственным интегрированием (суммированием) потерь мощности по результатам d расчётов установившихся режимов для нагрузок – интервалов постоянства графиков нагрузок
|
|
(6) |
Сопоставление результатов расчёта представлено в таблице 3.
Таблица 3.
Результаты расчёта потерь ЭЭ
|
№ схемы |
KЗ |
KНР |
R |
ΔЭЭ, МВт∙ч |
ΔЭ2, МВт∙ч |
ΔЭО, МВт∙ч |
|
|
|
1 |
0,757÷ 0,790 |
0,604÷ 0,619 |
0,990÷ 0,999 |
20,310 |
20,300 |
20,804 |
-0,0473 |
2,433 |
|
2 |
0,801÷ 0,822 |
0,552÷ 0,618 |
0,653÷ 0,991 |
9,129 |
9,103 |
9,188 |
-0,285 |
0,655 |
|
3 |
0,662÷ 0,882 |
0,515÷ 0,745 |
0,461÷ 0,998 |
13,753 |
13,721 |
14,360 |
-0,234 |
4,415 |
|
4 |
0,832÷ 0,887 |
0,641÷ 0,805 |
0,762÷ 0,884 |
15,963 |
15,659 |
15,788 |
-1,904 |
-1,098 |
|
5 |
0,806÷ 0,841 |
0,689÷ 0,750 |
0,702÷ 0,986 |
4,688 |
4,682 |
4,656 |
-0,124 |
-0,676 |
|
6 |
0,688÷ 0,850 |
0,361÷ 0,741 |
0,841÷ 0,980 |
6,765 |
6,685 |
6,640 |
-1,180 |
-1,845 |
|
7 |
0,730÷ 0,841 |
0,378÷ 0,741 |
0,772÷ 0,977 |
53,464 |
53,254 |
53,229 |
-0,393 |
-0,440 |
|
8 |
0,503÷ 0,822 |
0,503÷ 0,697 |
0,728÷ 0,999 |
45,058 |
44,951 |
44,997 |
-0,237 |
-0,134 |
|
σx |
|
|
|
|
|
|
0,608 |
1,952 |
|
|
|
|
|
|
|
|
-0,545±0,496 |
0,110±1,591 |
Из представленных результатов (табл.3) относительная ошибка расчёта потерь ЭЭ в исследуемой экспериментальной совокупности, при использовании ОГН, полученных индивидуально для каждой отдельной схемы, находятся в диапазоне (-1,04 %; -0,0488 %). При этом средняя относительная ошибка расчёта ЭЭ, вычисленная с помощью обобщённых ОГН статистически представительной совокупности нагрузок, существенно не возрастает и находится в интервале (-1,48 %, 1,70 %). Данная погрешность приемлема для практических расчётов.
Выводы
1. Обобщённые ортогональные графики нагрузок, полученные методом главных компонент из статистически представительного множества графиков электрических нагрузок, являются статистически устойчивыми и могут рассматриваться как типовые, поскольку возможно их применение для восстановления графиков нагрузок, не входящих в обучающее множество исходных признаков, с достаточной для практических расчётов точностью.
2. Для восстановления (моделирования) графиков электрических нагрузок электроэнергетических систем практически без потери точности достаточно использовать от двух до четырёх обобщённых (типовых) ортогональных графиков нагрузок.

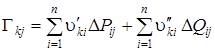 ,
, 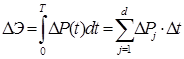 .
.