Изучение темы « Окружность: хорды и дуги » в 7 классе

Аннотация. Данная статья будет интересна учителям математики, работающим по учебнику «Геометрия. 7 класс. В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолов». В ней предла­гается основа урока по изучению новых понятий, связанных с окружностью.

Ключевые слова: окружность, дуга, хорда, центральный угол.

В школьном курсе математики с понятием окружности и ее основными элементами учащиеся знакомятся еще в начальной школе.

С началом изучения курса геометрии все накопленные ранее знания систематизируются, вводятся определения уже известных фигур, изучаются их свойства.

Данную статью можно взять за основу урока по изучению новых понятий, связанных с окружностью (хорда, дуга, центральный угол).

Вопросы:

— Ребята, какую геометрическую фигуру мы изучаем? (окружность)

— А что называется окружностью? (Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.)

— Как называется эта точка? (Точка О – центр окружности)

— Что такое радиус окружности? А что называется диаметром?

А как связаны между собой радиус и диаметр?

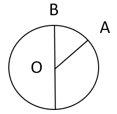
Рисунок 1. Иллюстрация

На доске начертить окружность и показать ее основные элементы (центр, радиус, диаметр)

1. Изучение нового материала.

— Ребята, а если взять на окружности две точки А и В и провести через них отрезок АВ, Будет ли этот отрезок являться диаметром? Почему?

А отрезок АВ больше или меньше диаметра?

А что общего у него с диаметром?

Отрезок АВ называется ХОРДОЙ.

В тетрадях ученики записали число, начертили окружность, хорду АВ и записали определение

ХОРДА – отрезок, соединяющий две точки окружности.

Хорда с греческого переводится «струна»

Открыть учебник на странице 82, найти рисунок 137.

Назвать отрезки, которые являются хордами, диаметром, радиусом.

Сформулировать еще раз определение хорды, диаметра, радиуса окружности.

— Ребята, посмотрите на рисунок 1 на доске. Какие еще геометрические фигуры вы здесь видите? (Угол)

— А что называется углом?

УГОЛ – это геометрическая фигура, состоящая из точки и двух лучей, исходящих из этой точки. Эта точка- общее начало двух лучей – называется вершиной угла, а сами лучи – сторонами угла.

— Назовите угол, который вы видите на рис.1 на доске.

— Угол ВОА, угол ВОС, угол АОС.

— А что общего у всех этих углов?

— Вершины этих углов расположены в центре окружности.

— Ребята, а какое бы вы предложили название для таких углов?

ЦЕНТРАЛЬНЫЙ УГОЛ – угол с вершиной в центре окружности.

Сделать чертеж в тетрадях. Угол СОК – центральный угол

— Ребята, а в каких единицах измеряют углы?( в градусах)

— А центральные углы тоже измеряют в градусах? Да.

— Вспомним еще раз определение окружности.

Начертить на доске дугу и окружность.

Дуга МN – часть окружности.

А теперь давайте откроем учебник на стр. 82, посмотрим на рис. 138. Мы видим две дуги: APB и AQВ. Эти дуги ограничены точками А и В.

— А как определить размер дуги?

Величина дуги равна величине центрального угла, который на нее опирается.

Записать в тетрадях: дуга MKN = угол MON.

Пример (устно)

Если угол MON = 35, то дуга MKN = ? (35)

— А как найти большую дугу MPN?

— Надо из 360 вычесть градусную меру дуги MKN.

Дуга MPN = 360 - MKN.

Итак, запишем в тетрадях: сумма градусных мер двух дуг окружности с общими концами равна 360.

Давайте обобщим. Какие новые понятия мы узнали? (хорда, дуга, центральный угол)

Домашнее задание: п. 30 стр. 82, упр. 103.

Но есть и учебники по геометрии других авторов, в которых тема «Окружность» освящается по-другому. Так, в учебнике А.В. Погорелова понятие «Окружность» вводится в 7 классе в теме

«Геометрические построения». Здесь же даются понятия хорды, диаметра, радиуса окружности, а также окружности, описанной около треугольника и вписанной в него.

А вот вписанный и центральный углы А.В. Погорелов рассматривает в 9 классе при изучении темы «Многоугольники».

Причем определение центрального угла дается как «угол, под которым видна сторона правильного многоугольника из его центра». А в учебнике Бутузова В.Ф. «угол с вершиной в центре окружности называется ее центральным углом».

Учащиеся, которые занимаются по программе «Школа 2000» под редакцией Л.Г. Петерсон, с понятием окружности, радиуса и диаметра впервые знакомятся во 2 классе.

Поэтому урок геометрии по теме «Окружность и ее элементы» для них является, с одной стороны, уроком изучения нового материала, а с другой стороны, повторением уже изученного ранее и закреплением этих знаний.