Построение математической модели экономики германии и анализ ситуации вызванной COVID-19

BUILDING A MATHEMATICAL MODEL OF THE GERMAN ECONOMY AND ANALYZING THE SITUATION CAUSED BY COVID-19

Natalia Lyamicheva

Student, Peoples' Friendship University of Russia, Russian Federation, Moscow

Аннотация. Работа включает в себя описание динамической модели Рамсея и дает возможность изучить результаты ее идентификации, а также спрогнозировать поведение экономики в следствии COVID-19 для экономики Германии. Способ идентификации модели реализован на оценке близости расчетных и статистических временных рядов макроэкономических показателей.

Abstract. The paper includes a description of the Ramsey dynamic model and provides an opportunity to study the results of its identification, as well as to predict the behavior of the economy in the context of COVID-19 for the German economy. The method of model identification is based on the estimation of the proximity of calculated and statistical time series of macroeconomic indicators.

Ключевые слова: модель Рамсея, экономика Германии, инвестиции, макроэкономика, динамическая модель, COVID-19.

Keywords: Ramsey model, German economy, investment, macroeconomics, dynamic model, COVID-19.

Введение

Германия – экономически развитая страна с высоким уровнем жизни. Но в данной момент переживает как и весь мир вспышку опасного заболевания COVID-19. Построение такой модели может описать, как следует дальше вести экономическую политику.

1. Описание модели

Построим и идентифицируем параметры математической модели экономики ФРГ. Для этого возьмем временные ряды данных за 1970-2018 гг. для макроэкономических показателей ФРГ (X = Y, I, C, J, E) в национальной валюте (national currency) в текущих ценах (curent prices) и в постоянных ценах 2015 г. (constant prices), а также численность населения (N(t)=Population) с сайта ООН [1].

Введем обозначения, которые будут использоваться далее и не будут упоминаться в ходе повествования:

С = расходы на конечное потребление; для 2015 года: С₂₀₁₅ ;

J = валовое накопление капитала; для 2015 года: J₂₀₁₅ ;

Е = экспорт товаров и услуг; для 2015 года: E₂₀₁₅;

I = импорт товаров и услуг; для 2015 года: I₂₀₁₅;

Y = валовой внутренний продукт (ВВП); для 2015 года: Y₂₀₁₅;

N(t) = численность населения страны ;

 — валовой внутренний продукт;

 — число людей, участвующих в экономике;

 — количество капитала в экономике ФРГ; K₀ – начальный капитал;

, – параметры;  — время (год).

Для рассмотрения динамической модели Рамсея [3] возьмем для начала производственную функцию Кобба — Дугласа [4]:

При этом далее ограничим параметры для функции . Предполагаем, что труд изменяется с неизменным темпом (2), а труд по формуле (3):

Тогда в любой момент времени t верна формула для основного макроэкономического баланса в текущих ценах [5]:

где p^Y – дефлятор ВВП, ,  – индексы цен на импорт, конечное потребление, инвестиции и экспорт соответственно. Предположим, что

Поделив тогда обе части балансового уравнения на дефлятор ВВП получим уравнение в текущих ценах

где относительная цена на инвестиции  некая функция времени и двух параметров ;

некая функция времени и двух параметров, определяемая по подгонке к статистике на инвестиции .

Задача заключается в поиске функций  и J(t). Пусть

Отсюда легко находим  и подбираем к ней функцию максимально её аппроксимирующую. Подставив всё в модель, найдем  и подберем к ней тоже максимально аппроксимирующую её функцию .

Затем построим графики и

2. Построение модели

Этап 1. Найдем индексы цен, . Строим графики цен  для  по .

Рисунок 1. Индексы цен

Этап 2. Найдем и построим график удельных показателей по времени от 1970 до 2018 года, используя формулу:

Рисунок 2. Удельные показатели

Этап 3. Найдем данные по труду , , млн. человек.

Этап 4. Рассчитаем простейшую модель при текущих параметрах, имеющих нижнюю и верхнюю границы: , , ,  Посчитаем , , ,

Будем искать функцию  пока не получим максимально близкую функцию к . Затем произведём поиск параметров простейшей динамической модели (в постоянных ценах 2015 г.) по близости расчетных и статистических данных на интервале 2010-2018 по . Задача заключается в подборе двух динамических функций S и Q.

На следующих графиках представлен результат:

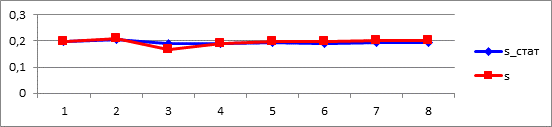
Рисунок 3. График и

Рисунок 4. График

3. Пандемия, вызванная COVID – 19 и экономика

Германия  –  это «локомотив Евросоюза», т.е. страна, которая должна поддерживать другие страны ЕС для стабильной работы механизма своей страны. Серьезная пандемия, которая вызвана смертельно опасным вирусом COVID – 19 в первую очередь нарушает экономические отношения между Китаем, Германией и странами ЕС вообще. В связи с COVID – 19  происходит закрытие границ для туристов, что отнимает у Германии огромную экономически прибыльную отрасль.

Из-за сложившейся эпидемиологической ситуации, государство имеет серьезные проблемы с поставками. Так, например, два крупных лидера компаний пароходства Maersk и Cosco отменили за февраль 280 контейнеровозов. И в связи с этим в разнообразных областях стало не хватать деталей для производства. На данный момент речь не идет о полной остановке международных перевозок, но они очень сильно затруднены. Как и все страны Германия имеет  «подушку безопасности» и здесь стоит вопрос о том, насколько она просядет. Так же экономист Deutsche Bank Давид Фолькертс – Ландау считает, что из кризиса выйдут две страны: Китай и ФРГ. Конечно, сейчас рано делать какой либо вывод или говорить о точных процентах, так как пандемия еще не закончилась, но можно попробовать рассчитать примерную летальность и шанс на выживание, на основе данных, которые у нас есть.

Предположим, что 20 мая пандемия закончилась и посчитаем летальность и шанс на выживание.

Пусть  количество заболевших,  количество выздоравлений,  количество умерших,  число «определившихся»,  процент летальности,  шанс выжить в процентах. Число «определившихся» вычисляется по формуле:

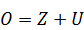                                                                                                              (3.1)

Рассчитаем процент летальности:

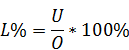                                                                                                        (3.2)

Рассчитаем шанс на выживание в процентах:

                                                                                                          (3.3)

Также рассчитаем процент смертности:

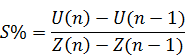                                                                                                    (3.4)

Таблица.

Таблица расчетных данных за одну неделю

По таблице построим график.

Рисунок 5. Динамика по трем показателям

Свяжем, наконец, модель Рамсея и ситуацию с COVID - 19.

Возьмем данные для: Общего объема ВВП 2018 и 2019 гг.; минимально прогнозируемых потерей общего объема ВВП; максимально прогнозируемых потерей общего объема ВВП; А также некоторые данные других годов, которые нужны будут для построения графиков.

Таблица 2.

Расчет min и max прогнозируемых потерь

Затем посчитаем процент падения ВВП по сравнению с 2019 годом.

1) минимальное падение в %: 8,14

2) максимальное падение в %: 19,81

Теперь предположим, что все макроэкономические показатели упадут с таким же темпом. Посчитаем,  чему они станут равны и построим графики. 

Рисунок 6. Изменения показателей при минимальных потерях

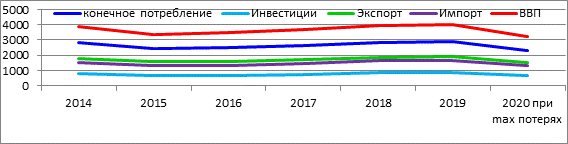
Рисунок 7. Изменения показателей при максимальных потерях

Итого, если основные макроэкономические показатели упадут с тем же темпом, что и ВВП, то можно ожидать, снижение остальных до показателей 2015 года (при максимальных и минимальных подсчетах). Довольно сильный откат, но всё-таки учитывая наличие подушки безопасности, возможно, мой прогноз окажется более суровый, чем действительность

Заключение. Были взяты статистические данные по Германии с 1970 по 2018 г. Далее сравнили расчетные временные ряды со статистическими рядами. Находим основные параметры. Параметры модели найдены с помощью аппроксимации отклонений между расчётными временными рядами макроэкономических показателей и соответствующими им статистическими данными. Затем проанализирована ситуация с Covid-19, таким образом модель можно использовать для прогноза поведения макроэкономических показателей Германии.