Кодек с использованием мажоритарного декодирования как один из способов исправления двукратных ошибок

1. Введение

Обеспечение достоверности передаваемой информации является одной из главных задач современных систем передачи информации. Для выполнения этой задачи в системах передачи информации используется помехоустойчивые кодеки. В настоящее время существуют различные виды помехоустойчивых кодеков, которые отличаются друг от друга используемыми для их реализации средствами, временными затратами на их применение, затратами дополнительного времени на передачу фиксированного объема данных (которое зависит от изменения объема трафика пользователя), степенью обеспечения достоверности передачи информации.

При использовании помехоустойчивого кодирования в системе связи в передаваемый цифровой поток вносится избыточность, с помощью которой возможно обнаружение и исправление возникших в результате влияния помех ошибок. Обеспечение достоверности передаваемой информации при наличии ошибок и вредного влияния помех играет важную роль в современных сетях передачи информации [1, 2].

В статье предлагается рассмотреть кодек с использованием мажоритарного декодирования, направленный на исправление двукратных ошибок. Для исследования был выбран код (10, 4), который содержит 4 информационных и 6 проверочных битов.

2. Линейные блочные коды

Блочное кодирование. При использовании в системе блочного кодирования происходит разбиение входной информации на блоки, состоящие из k символов. Впоследствии по определенному закону происходит преобразование этих блоков в n-символьные, где n>k. Избыточно введённые биты, количество которых равно (n-k), называются битами чётности [3].

На рисунке 1 представлена схема кодирования.

Рисунок 1. Схема блочного кодирования (10, 4)

Как видно из рисунка 1 проверочные биты (r) формируются с помощью операции сложения по модулю 2 определённых информационных битов (i).

Приведём пример. Предположим, что необходимо закодировать следующую комбинацию: 1101. Кодирование происходит путём перемножения передаваемого сообщения и генерирующей матрицы:

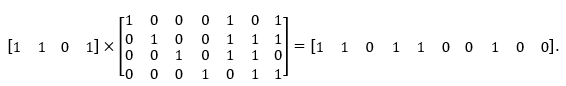
Таким образом, после применения кодирования по каналу связи будет передаваться комбинация [1101 100100].

Мажоритарное декодирование. В проектируемой модели используется мажоритарное декодирование, суть которого состоит в мажоритарном оценивании веса ошибки, произошедшей в i-м символе кодового слова. Подобная оценка проводится с помощью проверочных уравнений [4].

Для нахождения проверочных уравнений 2-го и последующих кодовых символов удобно использовать проверочные уравнения, найденные для 1-го кодового символа.

Рассмотрим процесс мажоритарного декодирования на примере исследуемого кода. Ниже представлена система проверочных уравнений для каждого из 4-х информационных символов (x(i) – значения символов кодового слова на входе декодера):

Исправление кратных ошибок. Рассмотрим декодирование при возникновении двукратных ошибок на примере символа из предыдущего примера. Допустим, что из-за шумов в канале произошла двукратная ошибка, например, в 1-м и 3-м кодовых символах. Значит, на вход декодера поступает [0111 100100].

В ходе исследования было выявлено, что использование мажоритарного декодера с рассмотренной ранее системой из 15 проверочных уравнений обладает хорошей помехоустойчивостью, однако, он не позволяет бороться с кратными ошибками. После анализа литературы, для борьбы с кратными ошибками система проверочных уравнений была уменьшена. Уравнения были выбраны из ранее найденных с условием: в состав уравнений входит нечётное число информационных бит или только проверочные. Тогда системы проверочных уравнений имеют следующий вид:

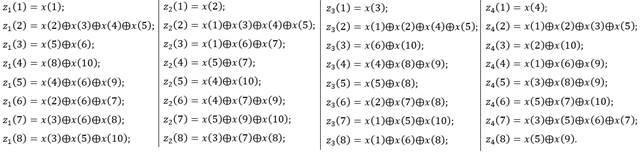
Определим с помощью проверочных уравнений значения z_i для каждого из информационных символов и примем решение, какое значение (1 или 0) передавалось:

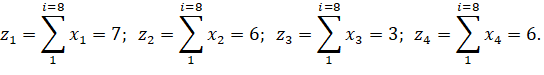
Т.к. при мажоритарном декодировании решение о символе принимается голосованием по большинству, то установив порог в 4, получаем декодированную последовательность [1101]. Декодирование совершенно верно.

3. Реализация кодека

Практическая реализация мажоритарных декодеров привлекательна высоким быстродействием и низкой сложностью. На рисунке 2 представлена схема кодека, собранная в системе моделирования Simulink.

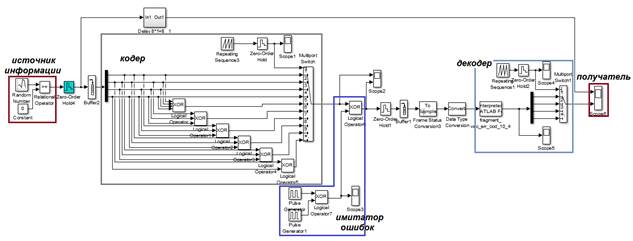
Рисунок 2. Модель исследуемого кодека в Simulink

Источник сигнала представлен блоком Random Number, который с помощью блоков Relational Operator и Constant превращается в однополярную последовательность. Блок Buffer исполняет роль запоминающего устройства. Далее происходит формирование символов, состоящих из 4-х битов. Блоки Logical Operator помогают сформировать проверочные символы из информационных.

Мажоритарный декодер реализован с использованием блока MatLab Fcn. Данный блок содержит функцию с системами проверочных уравнений. Здесь же происходит исправление ошибок, если таковые возникли при передаче. В соответствии с рассматриваемой схемой, исправляются лишь ошибки, которые произошли в информационной части.

Также, данная модель содержит имитатор ошибок, который состоит из Pulse Generator (генератор импульсов) и XOR (сумматор по модулю 2). С его помощью можно задать ошибки в последовательности, чтобы проверить правильность работы разрабатываемого мажоритарного декодера.

С помощью имитатора зададим ошибки в 1-м и 3-м бите. На рисунке 3 для сравнения представлены осциллограммы сигналов: сигнал источника (сверху) и сигнал после декодирования (снизу).

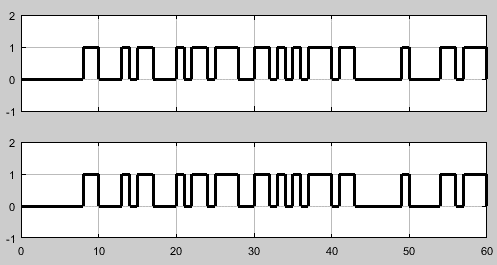
Рисунок 3. Осциллограммы сигналов для сравнения

Как видно из рисунка 3, декодирование было произведено верно.

В ходе эксперимента кодек был включён в состав QPSK-модема. Для оценки исправляющей способности в модель были включены 2 детектора ошибок. Модель показала следующие результаты: примерно на 6 ошибок канала передачи приходится 1 ошибка декодера. Энергетический выигрыш данной модели составил ∼ 1,8 дБ.