Статья:
ВЫБОР ИНТЕЛЛЕКТУАЛЬНОЙ СИСТЕМЫ ДИАГНОСТИКИ ДЛЯ ИНТЕЛЛЕКТУАЛЬНОГО АНАЛИЗА ДАННЫХ ПРИ ИСПЫТАНИЯХ ТУРБОРЕАКТИВНОГО ДВИГАТЕЛЯ
Конференция: CLXX Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Технические науки
Выходные данные
Елизарова А.А. ВЫБОР ИНТЕЛЛЕКТУАЛЬНОЙ СИСТЕМЫ ДИАГНОСТИКИ ДЛЯ ИНТЕЛЛЕКТУАЛЬНОГО АНАЛИЗА ДАННЫХ ПРИ ИСПЫТАНИЯХ ТУРБОРЕАКТИВНОГО ДВИГАТЕЛЯ // Молодежный научный форум: электр. сб. ст. по мат. CLXX междунар. студ. науч.-практ. конф. № 19(170). URL: https://nauchforum.ru/archive/MNF_interdisciplinarity/19(170).pdf (дата обращения: 23.04.2024)
Лауреаты определены. Конференция завершена
Эта статья набрала 0 голосов
Мне нравится0
Дипломы
лауреатов
лауреатов
Сертификаты
участников
участников
Дипломы
лауреатов
лауреатов
Сертификаты
участников
участников
CLXX Студенческая международная научно-практическая конференция «Молодежный научный форум»
ВЫБОР ИНТЕЛЛЕКТУАЛЬНОЙ СИСТЕМЫ ДИАГНОСТИКИ ДЛЯ ИНТЕЛЛЕКТУАЛЬНОГО АНАЛИЗА ДАННЫХ ПРИ ИСПЫТАНИЯХ ТУРБОРЕАКТИВНОГО ДВИГАТЕЛЯ
Елизарова Анна Александровна
магистрант, ФГБОУ ВО Уфимский государственный авиационный технический университет, РФ, г. Уфа
Саитова Гузель Асхатовна
научный руководитель, доцент каф. техн. кибернетики,
ФГБОУ ВО Уфимский государственный
авиационный технический университет,
РФ, г. Уфа
Аннотация. Процесс оптимизации анализа данных с испытаний предлагается осуществлять с помощью интеллектуального анализа данных блока электронной системы управления (ЭСУ). При разработке интеллектуальной системы для начала необходимо выбрать наиболее подходящую с помощью метода анализа иерархий.
Ключевые слова: искусственный интеллект, система анализа данных, ТРД, метод анализа иерархий.
Актуальность исследования обоснована необходимостью анализа данных с испытаний турбореактивного двигателя и принятия решений в сложных ситуациях.
На начальных этапах разработки системы диагностики должен быть сделан выбор интеллектуальной системы. Таким образом, можно использовать метод анализа иерархий.
Метод анализа иерархий является систематической процедурой для иерархического представления элементов, определяющих суть проблемы.
Данный метод является замкнутой логической конструкцией, обеспечивающей с помощью простых правил анализ сложных проблем во всем их разнообразии и приводящей к наилучшему ответу. К тому же, применение метода позволяет включить в иерархию все имеющееся у исследователя по рассматриваемой проблеме знание и воображение [1].
В качестве экспертов были выбраны три человека: магистрант Елизарова Анна, аспирант Елизарова Анастасия, также работник предприятия, задействованный в разработке.
Иерархическая структура выбора системы управления представлена на рисунке 1.
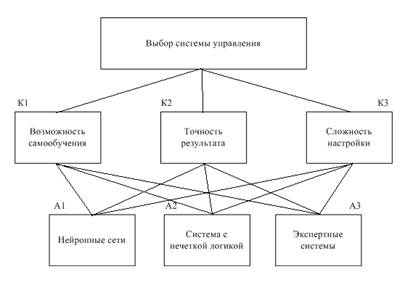
Рисунок 1. Иерархическая структура выбора типа нейронной сети
Применим метод парных сравнений для определения приоритетов всех элементов иерархий. В таблице 1 представлены матрицы сравнений альтернатив по критериям и сравнение самих критериев.
Талица 1.
Матрицы парных сравнений
|
Матрица парных сравнений альтернатив по первому критерию |
|||||
|
Возможность самообучения |
А1 |
А2 |
А3 |
Компоненты собственного вектора |
Нормализованный вектор приоритетов |
|
А1 |
1 |
7 |
9 |
3,98 |
0,785 |
|
А2 |
1/7 |
1 |
3 |
0,754 |
0,149 |
|
А3 |
1/9 |
1/3 |
1 |
0,333 |
0,066 |
|
Сумма |
1,253 |
8,33 |
13 |
5,067 |
|
|
λ=3,083, ИС=0,0415;ОС=0,07 |
|||||
|
Матрица парных сравнений альтернатив по второму критерию |
|||||
|
Точность результата |
А1 |
А2 |
А3 |
Компоненты собственного вектора |
Нормализованный вектор приоритетов |
|
А1 |
1 |
4 |
6 |
2,88 |
0,63 |
|
А2 |
1/4 |
1 |
3 |
0,9 |
0,197 |
|
А3 |
1/6 |
1/3 |
1 |
0,79 |
0,173 |
|
Сумма |
1,42 |
5,33 |
10 |
4,57 |
|
|
λ=3,067, ИС=0,0335;ОС=0,057 |
|||||
|
Матрица парных сравнений альтернатив по третьему критерию |
|||||
|
Сложность настройки |
А1 |
А2 |
А3 |
Компоненты собственного вектора |
Нормализованный вектор приоритетов |
|
А1 |
1 |
5 |
6 |
3,1 |
0,725 |
|
А2 |
1/5 |
1 |
2 |
0,74 |
0,173 |
|
А3 |
1/6 |
1/2 |
1 |
0,436 |
0,102 |
|
Сумма |
1,37 |
6,5 |
9 |
4,276 |
|
|
λ=3,036, ИС=0,018;ОС=0,031 |
|||||
|
Матрица парных сравнений критериев |
|||||
|
|
К1 |
К2 |
К3 |
Компоненты собственного вектора |
Нормализованный вектор приоритетов |
|
К1 |
1 |
4 |
2 |
2 |
0,546 |
|
К2 |
1/4 |
1 |
1/4 |
0,4 |
0,1 |
|
К3 |
1/2 |
4 |
1 |
1,26 |
0,354 |
|
Сумма |
1,75 |
9 |
3,25 |
3,66 |
|
|
λ=3,006, ИС=0,003;ОС=0,005 |
|||||
Далее определили наилучшую альтернативу:
Таким образом наилучшая альтернатива – Нейронные сети.
В данной работе была выбрана интеллектуальная система.
Список литературы:
1. Саати, Т.Л. Принятие решений. Метод анализа иерархий // Т.Л. Саати.−М.: Радио и связь, 1993 − 278 с.
