РАЗВИТИЕ И ПРИМЕНЕНИЕ АЛГОРИТМОВ МАШИННОГО ОБУЧЕНИЯ В АНАЛИЗЕ ДАННЫХ

Аннотация. В данной статье рассматривается актуальная проблематика развития и применения алгоритмов машинного обучения в анализе данных. В современном мире огромное количество данных накапливается ежедневно в различных областях, и их анализ становится всё более важным для принятия обоснованных решений. Алгоритмы машинного обучения позволяют автоматизировать процесс анализа данных, выявлять скрытые закономерности и делать прогнозы на основе имеющихся данных. В статье рассматривается исторический обзор развития алгоритмов машинного обучения, основные принципы и методы, а также их применение в современном мире. Также обсуждаются вызовы и перспективы использования алгоритмов машинного обучения в анализе данных. Также приведен пример анализа данных с помощью корреляционного анализа.

Ключевые слова: машинное обучение, прогнозирование, алгоритмы, данные.

С появлением больших данных (Big Data) в последние десятилетия объемы информации, генерируемой и накапливаемой в различных областях, значительно возросли. Этот взрыв данных создал новые возможности и вызвал новые вызовы для анализа и использования информации. В ответ на этот вызов алгоритмы машинного обучения стали широко применяться для анализа данных, предоставляя возможность автоматизировать процессы анализа, выявлять закономерности и строить прогнозы на основе имеющихся данных [1].

Исторический обзор развития алгоритмов машинного обучения

Алгоритмы машинного обучения имеют долгую историю развития, начиная с классических методов, таких как линейная регрессия и метод k-ближайших соседей, и заканчивая современными нейронными сетями и глубоким обучением. Важными этапами в развитии машинного обучения были появление алгоритмов деревьев решений, метода опорных векторов (SVM), алгоритмов кластеризации и обучения с подкреплением [2]. Открытие новых методов и алгоритмов, а также улучшение вычислительных ресурсов, способствовало расширению областей применения машинного обучения.

Принципы и методы машинного обучения

Основными принципами машинного обучения являются обучение на основе данных (data-driven learning) и обобщение (generalization). Для обучения моделей машинного обучения используются различные методы, такие как надзорное (supervised), ненадзорное (unsupervised) и полу-надзорное (semi-supervised) обучение. В зависимости от характера данных и задачи, на решение которой направлен анализ данных, выбирается соответствующий метод обучения.

Применение алгоритмов машинного обучения в анализе данных

Алгоритмы машинного обучения находят широкое применение в различных областях, таких как финансы, медицина, биология, маркетинг и многие другие [3]. В финансовой сфере, например, алгоритмы машинного обучения используются для прогнозирования цен на акции, выявления мошенничества, управления портфелем и других задач. В медицине алгоритмы машинного обучения применяются для диагностики заболеваний, прогнозирования эффективности лечения и других задач.

Вызовы и перспективы

Несмотря на значительные достижения в области машинного обучения, остаются нерешенными некоторые проблемы, такие как интерпретируемость моделей, недостаточная обработка неструктурированных данных и проблемы безопасности данных [4]. Однако с развитием вычислительных технологий и появлением новых методов машинного обучения, таких как глубокое обучение, открываются новые перспективы для решения этих вызовов

Данная работа основана на анализе образца данных Youtube_data.csv, загруженного с kaggle.com. Файл содержит информацию о видео на YouTube, включая id, название, канал, время публикации, количество просмотров, лайков, дизлайков, комментариев и страну. В работе проводится анализ данных, включая создание диаграммы рассеяния, проверку нормальности распределения выбранной переменной, оценку симметрии и эксцесса распределения, а также расчет коэффициентов корреляции между переменными. Полученные результаты помогают понять структуру данных и возможные взаимосвязи между ними.dat <-  read.csv('Youtube_data.csv')

Полученный код:

table(dat$channel_title)

table(dat$views)

dat$channel_title1 <- ifelse((dat$channel_title == 'HBO')|(dat$channel_title == 'WIRED')|

                             (dat$channel_title == 'SelenaGomezVEVO'), dat$channel_title, 'Others')

ctable <- table(dat$channel_title1, dat$views)

ctable

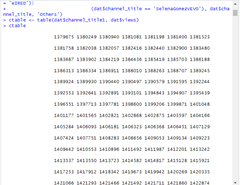
Рисунок 1. Таблица сопряженности

С помощью команды plot(dat$views, dat$likes) построим диаграмму (рисунок 2)

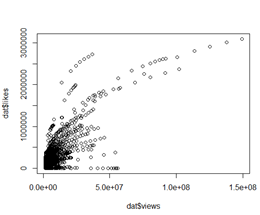
Рисунок 2. Диаграмма рассеяния между интервальными переменными: Просмотры и Лайки

Мы видим зависимость: чем больше просмотров, тем больше лайков. Выбросов, как таковых нет, значения распределяются по зависимости.

Выполнили тест хи-квадрат:

#Гипотезы:

#H0: не существует взаимосвязи между количеством просмотров на видео и количеством лайков на видео

#H1: существует взаимосвязь между количеством просмотров на видео и количеством лайков на видео

Рисунок 3. Тест хи-квадрат

Полученное p-значение больше 0.1 (равно 0.4813), что позволяет принять гипотезу H1 – следовательно, существует связь между количеством просмотров на видео и количеством лайков на видео.

Найдем ассиметрию и эксцесс, подключимся к библиотеке "moments" (рисунок 4):

Асимметрия и эксцесс - показатели, характеризующие геометрическую форму распределения. Асимметрия характеризует меру скошенного графика влево / вправо, а эксцесс – меру его высоты [4].

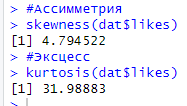
Рисунок 4. Асимметрия и аксесс

Ассиметрия и эксцесс являются положительными. Рассчитаем коэффициенты корреляции:

Корреляционный анализ – статистический метод, позволяющий с использованием коэффициентов корреляции определить, существует ли зависимость между переменными и насколько она сильна. Коэффициент корреляции – двумерная описательная статистика, количественная мера взаимосвязи (совместной изменчивости) двух переменных [5].

Таблица 1

Коэффициенты корреляции

Алгоритмы машинного обучения играют все более важную роль в анализе данных, обеспечивая возможность автоматизировать процессы анализа и прогнозирования на основе имеющихся данных. Развитие и применение алгоритмов машинного обучения продолжает продвигать границы того, что возможно в области анализа данных, и открывает новые возможности для принятия обоснованных решений в различных областях человеческой деятельности.