Идентификация состояния работы электрооборудования

Современное оборудование характеризуется сложностью и высокой стоимостью текущего обслуживания. Процесс его эксплуатации превратился в комплексную проблему, при решении которой необходимо одновременно учитывать управленческие, производственные, финансовые, технические и кадровые факторы.

Из литературы известны многочисленные определения аксиоматического выбора. В работах приводятся системы аксиом, по-разному определяющие понятия рационального агрегирования критерия в многокритериальной задаче. 

Обычно используют эти понятия для построения модели задачи принятия решения в аварийной ситуации и формирования способов ее решения.

В задаче математического программирования требуется вычислить мерный вектор , оптимизирующий критерий качества решения  при соблюдении ограничений 

где   - известные скалярные функционалы,

 -заданные числа,

  -заранее заданное множество n-мерного пространства.

То есть, задача математического программирования имеет вид:

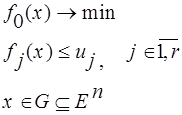
В зависимости от свойств функций  и свойств множества   имеют дело с тем или иным классом задач оптимизации.

В рассматриваемой задаче аварийного регулирования решением является выбор параметров сети (путем частичного или полного прикрытия некоторых задвижек и изменения режимов работы насосных станций), обеспечивающих подачу воды в аварийную зону, не превышающую допустимый уровень (возможно, нулевой). Множество регулируемых параметров не наделено естественной линейной структурой, а попытка вложить его в какое-либо пространство не является эффективной, поскольку, вообще говоря, множество решений не обязано быть выпуклым или хотя бы представляться в виде конечного объединения выпуклых множеств.

Более предпочтительным является учет того, что множество задвижек конечно, а степень их прикрытия можно дискретизировать по количеству витков задвижки (что обычно и делается на практике). Тем самым, мы получаем конечное число решений, т. е.  дискретное множество. Кроме того, существует конечное число стратегий по устранению аварий  (ремонтно-восстановительных работ). Таким образом, исследуемая задача должна быть отнесена к специальному разделу математического программирования - дискретному программированию.  При конечном числе альтернатив  можно всегда выбрать лучший вариант, перебирая альтернативы и сравнивая их между собой.

Oценена информационная сложность различных задач математического программирования. В частности, в этой работе аргументирована бесперспективность поиска универсальных методов решения любых невыпуклых задач. Поэтому является целесообразным разрабатывать специальные методы, учитывающие структуру и специфику более узких классов задач.

Необходимо также учитывать, что при формализации задач теории выбора решений, связанных с достижением многих целей, возникают определенные трудности концептуального характера, связанные с невозможностью построения единого (скалярного) критерия. Одним из наиболее эффективных способов разрешения этих трудностей является использования понятия "компромисс". Первый класс связан с использованием зарекомендовавших себя на практике механизмов выбора - содержательно оправданных процедур решения. Второй класс, реализующий аксиоматический подход к установлению понятия " компромисс" сводится к разработке и формулированию интуитивно рациональных требований к этому понятию и к доказательству существования процедур, удовлетворяющим таким требованиям. Задание некоторых функций выбора, указывающих для разных ситуаций из заданного множества предъявлений подходящий выбор, определяет третий класс путей согласования различных целей. Между всеми тремя подходами существует связь, все подходы могут быть описаны в терминах функции выбора.