Планирование движения автономного мобильного робота

Навигационные системы автономного мобильного робота (АМР), все больше применяются для навигации и выполнения целенаправленных задач в сложных областях и в различных пространствах. Хотя нечеткие системы были успешно применены в большом количестве приложений, они испытывают недостаток в способности извлекать знания из набора обучающих данных. Гибридная технология, разработанная путем объединения нечетко-логической системы поиска с возможностями генетического алгоритма (ГА) должна привести к выбору оптимального маршрута до заданного пункта.

В данном докладе предлагается применение метода нечетко-генетического управления АМР для моделирования в неструктурированной (неизвестной) окружающей среде при следующих ограничениях и допущениях:

• Двумерная окружающая среда делится на квадраты;
• Робот сканирует информацию до 6 квадратов сетки;
• Движение робота ограничивают только статические препятствия.
• Препятствия представлены занимаемой сеткой;
• Робот движется с постоянной скоростью;

Для решения задачи нечеткого логического управления (НЛУ)  роботом применяем алгоритм Мамдани. Данный алгоритм описывает несколько последовательно выполняющихся этапов и состоит из следующих блоков.

• Блок фаззификации (БФ) - процедура нахождения значений функции принадлежности нечетких множеств (термов) на основе обычных (четких) исходных данных. Разделим расстояние равное 6-ти квадратам на подмножества со следующими термами: далеко (Д), среднее (С), близко (Б) и очень близко (ОБ). Вокруг робота, область будет сканироваться на 360 ˚. Эта область будет разделена на восемь подмножеств со следующими термами: задний (З), задний левый (ЗЛ), левый (Л), передний левый (ПЛ), передний (П), передний правый (ППр), правый (Пр), задний правый (ЗПр). Функции принадлежности (ФП) представляют собой графическое представление входных и выходных подмножеств. В НЛУ используются одни и те же ФП для входных и выходных подмножеств, и допускает два входных подмножества для одного набора правил и четыре для другого набора правил.

Рисунок 1. Графическое представление БФ

• База знаний (БЗ) - происходит формирование базы правил вида «α есть β» с помощью связок «И», «ЕСЛИ - ТО». База знаний для НЛУ состоит из двух наборов нечетких продукционных правил для прямолинейного движения и преодоления препятствий. Набор для прямолинейного движения будет состоять из 24 нечетких правил следующего вида:

ЕСЛИ угол движения к цели передний И расстояние движения далеко, ТО нужное направление является переднее и желаемое расстояние далеко.

Набор для объезда препятствий будет состоять из 168 нечетких правил следующего вида:

ЕСЛИ угол движения к цели передней, расстояние движения очень близко И угол поворота передний левый, расстояние движения далеко, ТО нужное направление передний левый и желанное расстояние далеко.

При формировании базы знаний (192 правила) системы нечеткого вывода задаются весовые коэффициенты для каждого правила.

• Блок рассуждений (БР) – вычисляются степени истинности и принадлежности левых частей, модифицируются подмножества правой части правила в соответствии с левой частью методом  «произведения», выполняется объединение (суперпозиция) модифицируемых подмножеств методом «максимума».
• Блок дефаззификации (БД) - процесс нахождения обычного (не нечеткого) значения выходной переменной. Результат дефаззификации определяется по методу центра тяжести, в котором значение i-ой выходной переменной рассчитывается по формуле:

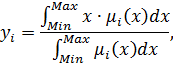
где:

 — функция принадлежности соответствующего нечеткого множества ;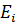

Min и Max — границы универсума нечетких переменных;

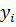 — результат дефаззификации.

Алгоритм примечателен тем, что он работает по принципу «черного ящика». На вход поступают количественные значения, на выходе они же. На промежуточных этапах используется аппарат нечеткой логики и теория нечетких множеств.

Очевидно, что робот нуждается в меньшем количестве правил, которые будут использоваться для достижения цели. Для нахождения оптимального набора правил используется ГА, основанный на механизмах естественного отбора и наследования. В этом подходе переменные, характеризующие решение, представлены в виде вектора генов. ГА генерирует новые решения как различные комбинации частей решений популяции, используя такие операторы, как отбор, рекомбинация (кроссинговер) и мутация.

В данной нечетко-генетической системе начальная популяция устанавливается случайным образом и численность популяции субъективна. С помощью функции пригодности (приспособленности) среди всех решений «популяции» выделяют наиболее подходящие решения. Которые  получают возможность «скрещиваться» и давать «потомство», а наихудшие решения удаляются из «популяции». Будем использовать следующую функцию пригодности правила:

П = М – К + (Ц*5) – (Р*5),

где

П – пригодность правила;

М – максимально допустимое число шагов робота;

К – количество шагов, робота для достижения к цели;

Ц – принимает положительное значение (+1), если удается достичь цели и отрицательное значение (-1), если это не удается. Умножается на 5 что бы увеличить значение пригодности;

Р – оставшееся расстояние от текущей позиции робота до целевой. Рассчитывается по следующей формуле: Р = ((текущая позиция - целевая позиция) / (исходное положение - конечное положение)) * 100. Умножается на 100 что бы увеличить результат.

Схемы кодирования базы знаний в генетической строке оказывают существенное влияние на эффективность ГА и играет важную роль в разработке методологии. Хотя большинство приложений ГА используют двоичный код для представления переменных, здесь следует использовать реальные значения (термы входных и выходных переменных нумеруются). Такая схема кодирования может кодировать каждую возможную комбинацию нечетких переменных в хромосоме и не подвергает ограничениям в отношении разработки нечетких правил.

Графическое представление предлагаемого метода изображено на рисунке 2.

Рисунок 2. Графическое представление метода

Для реализации нечетко-генетического алгоритма предлагается использовать объектно-ориентированный подход.

В качестве экспериментальной модели собран робот колёсный робот, составные части которого – микропроцессор, 3 колеса, серводвигатель, корпус и две кнопки под корпусом спереди и сзади робота. Кнопки являются датчиком столкновения с препятствием.