СЖАТИЕ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ РЯДОВ

Аннотация. В статье рассматриваются методы сжатия изображений на основе представления их в виде рядов. Основное внимание уделено разложению Фурье, дискретному косинусному преобразованию (DCT) и вейвлет-разложению. Описаны принципы работы этих методов, приведены математические формулы и примеры их применения в форматах сжатия изображений, таких как JPEG и JPEG 2000. Анализируются преимущества и ограничения каждого метода, а также их практическое использование в обработке цифровых изображений.

Ключевые слова: Сжатие изображений, ряды Фурье, дискретное косинусное преобразование, вейвлет-преобразование, обработка изображений, цифровая графика.

Сжатие изображений — это важная задача в обработке цифровой графики, направленная на уменьшение объёма данных при сохранении приемлемого качества изображения. Один из математических подходов к сжатию основан на представлении изображений в виде рядов, что позволяет эффективно уменьшать количество информации, необходимой для их хранения. В данной статье рассматриваются основные методы сжатия изображений с использованием рядов Фурье, разложения в ряды вейвлетов и других числовых представлений.

Разложение изображения в ряд Фурье основано на представлении функции яркости пикселей как суммы тригонометрических функций. Это позволяет выделять низкочастотные компоненты, отвечающие за основные элементы изображения, и отбрасывать высокочастотные компоненты, содержащие детали. Рассмотрим одномерное разложение в ряд Фурье 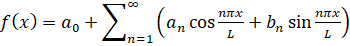(1):

,                                                                                 (1)

где коэффициенты Фурье вычисляются по формулам (2), (3):

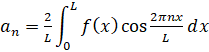,                                                                                                  (2)

                                                                                                  (3)

В двухмерном случае преобразование Фурье применяется к каждому измерению изображения отдельно. В реальных системах сжатия используется Дискретное Косинусное Преобразование (DCT), которое эффективно приближает ряд Фурье, но использует только косинусные составляющие.

Дискретное косинусное преобразование (DCT) является основой для форматов сжатия изображений, таких как JPEG. Оно позволяет представить изображение как сумму базовых косинусных функций разной частоты. Формула DCT для одномерного сигнала (4):

                                                                                               (4)

где 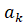 — нормирующий коэффициент.

Вейвлет-преобразование используется в форматах сжатия изображений, таких как JPEG 2000. В отличие от преобразования Фурье, которое анализирует изображение в глобальном масштабе, вейвлет-разложение позволяет выделять детали изображения на разных уровнях разрешения. Двумерное вейвлет-преобразование разлагает изображение на четыре поддиапазона: низкочастотный (LL), горизонтальные (LH), вертикальные (HL) и диагональные (HH) детали. На рисунке 1 показаны результаты двух шагов этого процесса для фотографии Ингрид Добеши (Ingrid Daubechies) (внесшей выдающийся вклад в теорию вейвлет-анализа). Коэффициенты расположены по правилу (таблица 1):

Таблица 1. Расположение коэффициентов

Например, LH означает, что в этом квадранте стоит результат применения фильтра низких частот к столбцам, высоких частот – к строчкам исходной матрицы, и прореживания вдвое по каждому направлению. На рисунке 1а более ярким цветом обозначены коэффициенты большей амплитуды. Четко видно, что их положение указывает на резкие перепады яркости. Такие перепады являются наиболее информативными при беглом просмотре любого изображения. Вейвлет-представление позволяет их локализовать путем последовательного уточнения, начиная с более крупных масштабов. Кроме того, коэффициенты проекции на различные пространства деталей отвечают за перепады яркости различной ориентации: например, если фильтр высоких частот применялся к строчкам, то в соответствующем квадранте ярче выделены вертикальные перепады. Это хорошо видно на рисунке 1б.

Для двухмерного изображения преобразование применяется отдельно по строкам и столбцам. После этого значительная часть коэффициентов может быть обнулена без сильной потери качества, что обеспечивает сжатие изображения. После разложения можно обнулить коэффициенты высокочастотных поддиапазонов, что приведёт к сжатию данных.

Самый простой подход к сжатию изображений при помощи вейвлет-преобразования состоит в следующем:

• Выполнить вейвлет-преобразование.
• Упорядочить коэффициенты.
• Отбросить “хвост” упорядоченного массива, энергия которого равна допустимой (по условиям задачи) величине.
• Запомнить сохраненные коэффициенты и их положение в массиве исходных коэффициентов.
• При восстановлении заменять отброшенные коэффициенты нулями.

Эта идея в той или иной форме присутствует во всех методах вейвлетного сжатия. Данную процедуру можно, например, применять раздельно к каждому из квадрантов, полученных при разложении по оптимально выбранным вейвлет-пакетам.

Рисунок 1а. Два уровня двумерного вейвлет-преобразования

Рисунок 1б. Полное дерево высоты 2 разложения по вейвлет-пакетам

Методы сжатия на основе рядов активно используются в цифровой обработке изображений. Формат JPEG использует DCT для разложения изображения на частотные компоненты и последующего квантования. Формат JPEG 2000 использует вейвлет-преобразование, позволяя добиваться более гибкого сжатия и лучшего качества (рис.2). Фильтрация изображений с помощью Фурье-преобразования позволяет устранять шум и улучшать качество.

Рисунок 2. Сравнение форматов сжатия

Методы сжатия изображений, основанные на разложении в ряды, позволяют значительно уменьшать объём хранимых данных без существенной потери качества. Разложение Фурье, дискретное косинусное преобразование (DCT) и вейвлет-преобразование являются основными инструментами, используемыми в современных алгоритмах сжатия.

Каждый из рассмотренных методов имеет свои преимущества и ограничения:

• DCT, применяемое в формате JPEG, эффективно работает для плавных градиентов, но может приводить к артефактам при высоком уровне сжатия.
• Вейвлет-преобразование, используемое в JPEG 2000, обеспечивает более гибкое сжатие и лучше сохраняет детали изображения.
• Фурье-преобразование находит применение в фильтрации изображений, устраняя шумы и улучшая качество.

Дальнейшие исследования в области сжатия изображений направлены на разработку адаптивных алгоритмов, которые смогут учитывать особенности конкретных изображений, минимизируя потери качества при высокой степени компрессии. Также перспективными направлениями являются гибридные методы, объединяющие преимущества различных преобразований, и использование нейросетевых подходов для оптимизации сжатия.