ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ ФОРМЫ МОЛЕКУЛЫ МЕТАНА

GEOMETRICAL MODELLING OF THE METHANE MOLECULE SHAPE

Irina Grigoreva

10th grade student of MBOU lyceum No.3, Russia, Irkutsk

Michael Perfileev

Scientific adviser, PhD in mathematics, Doctor of International Academy of Natural History, Russia, Irkutsk

Аннотация. Данная работа относится к области математической химии и посвящена геометрическому моделированию молекулы метана. Путем эмпирической проверки сотен вариантов подобрана функция, записанная в неявном виде и с высокой точностью воссоздающая форму молекулы метана. Таже при помощи оператора Лапласа (симметричного дифференциального оператора) записано дифференциальное уравнение, соответсвующее подобранной функции.

Abstract. This work pertains to the field of mathematical chemistry and is devoted to geometric modeling of the methane molecule. By means of empirical testing of hundreds of variants, a function is selected, written in implicit form and recreating the shape of the methane molecule with high accuracy. Also, using the Laplace operator (symmetric differential operator), a differential equation is written corresponding to the selected function.

Ключевые слова: метан, молекулярное моделирование, гибридизация орбиталей, синус, поверхность, оператор Лапласа

Keywords: methane, molecular modelling, orbital hybridisation, sine, surface, Laplace operator

Введение

Метан (болотный газ) - самый простой алкан, при нормальных условиях является бесцветным газом без вкуса и запаха, значительно легче воздуха, малорастворим в воде, основной компонент природного газа (77—99%).

Рисунок 1. Шаростержневая и шаровая модели молекулы метана

Атомы углерода в метане находятся в состоянии sp3-гибридизации и образуют четыре сигма-связи с атомами водорода, валентный угол между гибридными орбиталями равен 109,28^о [1]. То есть в молекуле метана происходит гибридизация орбиталей одного s-электрона и трёх p-электронов, в результате образуются 4sp3-гибридизованных электронных облака в форме деформированной объемной восьмёрки [2].

Рисунок 2. Условная схема образования -связей в молекуле метана

Длина ковалентной полярной C-H связи в молекуле метана равна 0,109 нм, энергия такой связи 413,7 кДж/моль [3].

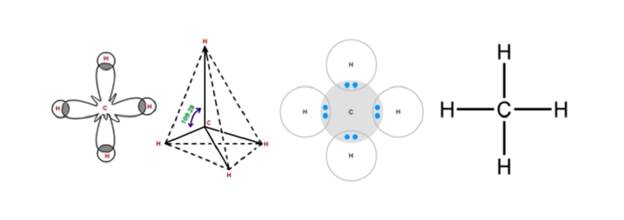
Рисунок 3. Различные схематические изображения молекулы метана

Цель данной работы - провести математическое моделирование формы молекулы метана при помощи неявной функции, записанной в виде трансцендентного уравнения. В качестве методов в работе использованы эмпирический подбор параметров уравнения поверхности и специализированные пакеты программ для построения трехмерных графиков функций.

Математическое моделирование формы молекулы метана

Рассмотрим функцию F трех переменных x, y, z , записанную в неявном виде при помощи трансцендентного уравнения, не разрешенного относительно этих переменных:

 ,                                                                                      (1)

где  и  - некоторые вещественные параметры. Таким образом,

 ,                                                                                 (2)

 .                                                                                                             (3)

Эмпирически проверкой сотен различных вариантов можно подобрать значения параметров  ;  .

Тогда уравнение (1) примет вид

 .                                                                                  (4)

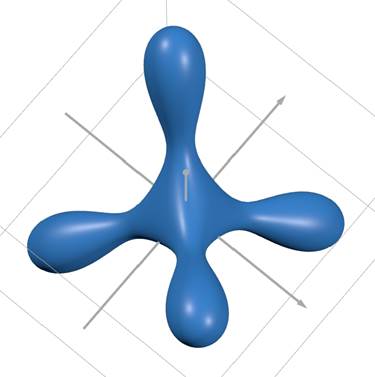
Рисунок 4. Результаты математического моделирования по формуле (4) под разными углами обзора

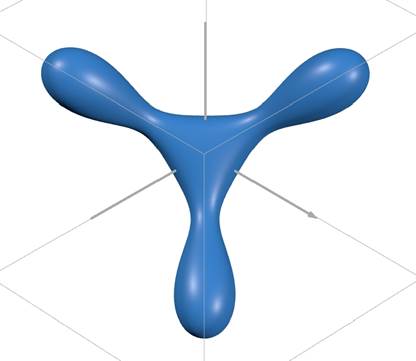
Рисунок 5. Результаты математического моделирования по формуле (4) под разными углами обзора

Рисунок 6. Результаты математического моделирования по формуле (4) под разными углами обзора

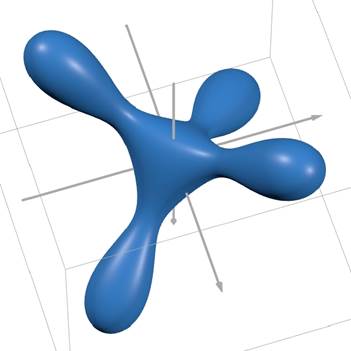
Рисунок 7. Результаты математического моделирования по формуле (4) под разными углами обзора

На риc. 4-7 изображены результаты математического моделирования по формуле (4) под разными углами обзора. Графики построены в специализированном пакете программ для построения трехмерных графиков.

Ползуясь правилами дифференцирования [4], легко получить выражения

 ;                                                                                         (5)

 ;                                                                                         (6)

 .                                                                                         (7)

Складывая равенства (5), (6), (7), получим

 ,                                                                                    (8)

где  - оператор Лапласа (лапласиан) — симметричный дифференциальный оператор, действующий на линейном пространстве гладких функций [5]. Оператор Лапласа ставит в соответствие функции F функцию

 .                                                                                                            (9)

Оператор Лапласа имеет широкое применение в математической физике, электростатике и электродинамике, квантовой механике.

Заметим, что выражения (4) и (8) обладают симметрией, как и сама молекула метана, имеющая форму правильного тетраэдра.

Заключение

Таким образом, в данной работе при помощи трансцендентного и дифференциального уравнений проведено математическое моделирование молекулы метана. В специализированном пакете программ для построения трехмерных графиков в соответствии с подобранной функцией построены графики в объеме под разными углами обзора, моделирующие форму молекулы метана.