Сравнение эффективности применения методов одномерного поиска в многомерных методах минимизации функций n переменных

Функция одной переменной, имеющая в интервале исследования [a,b] один оптимум, называется унимодальной [1].

Унимодальная функция не обязательно должна быть гладкой и даже непрерывной она может быть в некоторых точках интервала неопределенной. Предположение унимодальности не связано с жесткими ограничениями и выполняется во многих практических задачах поиска оптимума. Как правило, задачи одномерной оптимизации имеют унимодальную целевую функцию.

Последовательно сужая интервал исследования, в котором находится оптимальное значение искомой переменной, можно с достаточной степенью точности найти это оптимальное значение. Для этого необходимо выработать такую стратегию поиска, чтобы за меньшее число шагов (этапов) определить минимальный интервал, в котором лежит искомый оптимум, или свести исходный интервал до области заданной длины за минимальное число шагов [2].

К последовательным детерминированным методам поиска экстремума унимодальных функций относятся методы сканирования, дихотомии, золотого сечения и Фибоначчи.

Цель выполнения данной работы является выявление более эффективного метода среди применяемых методов дихотомии, золотого сечения и Фибоначчи. Нам необходимо исследовать их сходимость и провести сравнение по числу вычислений функции для достижения заданной точности.

Возьмем для примера следующую функцию: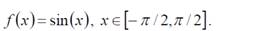

График функции показан на рисунке 1.

Рисунок 1. Графики функции

Нами была написана программа на языке C# :

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Linq;

using System.Text;

using System.Windows.Forms;

namespace WindowsFormsApplication6

{

    public partial class Form1 : Form

    {

        public Form1()

        {

            InitializeComponent();

        }

        //Функция

        public static double F(double x)

        {

            return Math.Sin(x);

        }

        //Погрешность

        double eps = 0.001;

        private void button1_Click(object sender, EventArgs e)

        {

            double a = -Math.PI / 2, b = Math.PI / 2, x1, x2;

            double c = eps / 2;

            int s = 0;

            while ((b - a) > eps)

            {

                x1 = (a + b) / 2 + c;

                x2 = (a + b) / 2 - c;

                if (F(x1) < F(x2))

                    a = x1;

                else b = x2;

                s = s + 2;

            }

            textBox1.Text = F((a + b) / 2).ToString();

            textBox2.Text = s.ToString();

        }

        private void button2_Click(object sender, EventArgs e)

        {

            double a = -Math.PI / 2, b = Math.PI / 2;

            double z = (1 + Math.Sqrt(5)) / 2;

            double x1 = b - (b - a) / z;

            double x2 = a + (b - a) / z;

            int s = 0;

            for (int i = 0; b - a > eps; i++)

            {

                if (F(x1) >= F(x2))

                {

                    a = x1;

                    x1 = x2;

                    x2 = a + b - x1;                 

                }

                else

                {

                    b = x2;

                    x2 = x1;

                    x1 = a + b - x2;                

                }

                s = s + 2;

            }

            double x = (a + b) / 2;

            double min = F(x);

            textBox3.Text = min.ToString();

            textBox4.Text = s.ToString();

        }

        private void button3_Click(object sender, EventArgs e)

        {

            double a = -Math.PI / 2, b = Math.PI / 2;

            double x1, x2, _x, xf1, xf2;

            int k = 0;

            int N = 0;

            double fn1 = 1, fn2 = 1, fn, f = (b - a) / eps;

            while (fn1 < f)

            {

                fn = fn1 + fn2;

                fn1 = fn2;

                fn2 = fn;

                ++N;

            }

            bool bix;

            int ix = N & 1;

            if (ix == 1)

                bix = true;

            else

                bix = false;

            x1 = a + (double)F(N - 2) / F(N) * (b - a) - (bix ? -1 : 1) * eps / F(N);

            x2 = a + (double)F(N - 1) / F(N) * (b - a) + (bix ? -1 : 1) * eps / F(N);

            xf1 = F(x1);

            xf2 = F(x2);

        P:

            ++k;

            if (xf1 >= xf2)

            {

                ix = (N - k) & 1;

                if (ix == 1)

                    bix = true;

                else

                    bix = false;

                a = x1;

                x1 = x2;

                xf1 = xf2;

                x2 = a + (double)F(N - k - 1) / F(N - k) * (b - a) + (bix ? -1 : 1) * eps / F(N - k);

                xf2 = F(x2);

            }

            else

            {

                ix = (N - k) & 1;

                if (ix == 1)

                    bix = true;

                else

                    bix = false;

                b = x2;

                x2 = x1;

                xf2 = xf1;

                x1 = a + (double)F(N - k - 2) / F(N - k) * (b - a) - (bix ? -1 : 1) * eps / F(N - k);

                xf1 = F(x1);

            }

            if (Math.Abs(b - a) <= eps)

            {

                _x = (a + b) / 2;

                textBox5.Text = F(_x).ToString();

                textBox6.Text = k.ToString();

            }

            else

                goto P;

        }

        static int F(int n)

        {

            int f, f1 =1, f2=1, m=0;

            while (m < n - 1)

            {

                f = f1 + f2;

                f1 = f2;

                f2 = f;

                ++m;

            }

            return f1;

        }    

        }

        }

Результат выполнения нашей программы показан на рисунке 2.

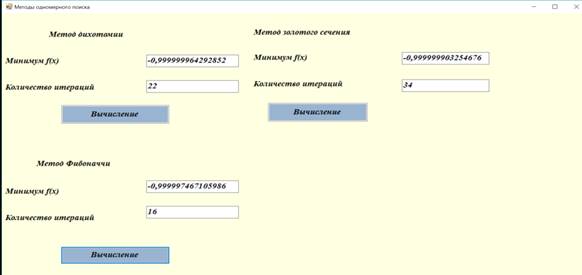
Рисунок 2. Результат применения методов

Вывод: было проведено ознакомление с методами одномерного поиска, используемыми в многомерных методах минимизации функций n переменных. Установлено что самым эффективным методом является метод Фибоначчи, с количеством вычислений функции равное 16. Второе место по эффективности занимает метод дихотомии, и самым неэффективным является метод золотого сечения.