Исследование зависимости времени дешифрования в криптосистеме RSA от параметров ключа
Конференция: LXXXII Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Физико-математические науки

LXXXII Студенческая международная научно-практическая конференция «Молодежный научный форум»
Исследование зависимости времени дешифрования в криптосистеме RSA от параметров ключа
Введение
Документооборот сейчас невозможно представить без электронной цифровой подписи. Подписанный квалифицированной электронной подписью документ имеет такую же юридическую силу, как и бумажный, который зафиксирован личной подписью и печатью [1].
Широкое распространение получили ЭЦП на основе алгоритма шифрования RSA. Этот алгоритм, основанный на том, что находить простые числа, даже большие - простая процедура, однако разложить на множители произведение двух чисел - нетривиальная задача. Он был разработан учеными из Массачусетского университета Р. Ривестом, А. Шамиром и Л. Адлеманом [2].
Актуальность данной работы обусловлена широкой областью применения электронной подписи и необходимостью разбираться в алгоритмах шифрования, чтобы предотвращать возможные атаки. Цель исследования: разработать программу, осуществляющую шифрование алгоритмом RSA и выявить зависимость времени дешифрования от параметров ключа.
Основные задачи исследования:
1. Провести аналитический обзор литературы.
2. Разработать программу на ЯП.
3. Провести модельные эксперименты сделать выводы.
Основная часть
RSA относится к системам шифрования с открытым ключом. То есть, для шифрования и расшифровки используются два ключа: открытый и секретный. Открытый ключ можно свободно передавать по любым каналам связи любым пользователям, в отличие от секретного ключа, который необходим для получения исходного сообщения. Неподверженность атакам алгоритма RSA возникла ввиду того, что перебором нелегко подобрать простые числа, дающие в произведении модуль n. Рассмотрим алгоритм подробнее. Его работа состоит из трех частей: генерация ключей; шифрование и дешифровка [3].
Генерация ключей:
1. Зафиксируем простые числа p и q.
2. Посчитаем их модуль n = p · q и функцию Эйлера φ(n) = (p − 1) · (q −1)
3. Произвольно выберем e так что, 2 ≤ e < n. Н.О.Д (n, e)=1. Где е - открытый ключ RSA.
4. Посчитаем d, 1 < d < n, который удовлетворят условию e·d mod φ(n)=1.
Шифрование:
чтобы закодировать сообщение M сделаем следующее:
1. Посимвольно разделим текст.
2. Заменим символы на их коды.
Закодируем последовательность, меняя код символа с на шифрокод:
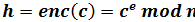
Расшифровка:
Декодируем последовательность, меняя шифрокод h на код 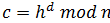 .
.
Заменим коды c на символы сообщения, тем самым восстановим его.
На основе литературы была разработана программа на языке C#, позволяющая производить шифрование и дешифровку. Выполнены модельные эксперименты по шифрованию и дешифровки сообщения для выявления зависимости времени дешифровки от выбора случайных простых чисел. Результаты эксперимента представлены в таблице 1.
Таблица 1.
Результаты эксперимента
|
Входные данные |
р |
q |
Выходные данные |
Время дешифрования, с |
|
«шифрование данных» |
5 |
7 |
«шифрование данных» |
1 |
|
«шифрование данных» |
23 |
29 |
«шифрование данных» |
1 |
|
«шифрование данных» |
101 |
103 |
«шифрование данных» |
2 |
|
«шифрование данных» |
211 |
223 |
«шифрование данных» |
8 |
|
«шифрование данных» |
311 |
313 |
«шифрование данных» |
31 |
|
«шифрование данных» |
409 |
419 |
«шифрование данных» |
175 |
Заключение
В ходе исследовательской работы был разработан алгоритм RSA, проведены модельные эксперименты и получены результаты. Можно заметить, что, увеличивая параметры ключа, заметно увеличивается и время дешифровки. Так, для значений p = 5 и q = 7 время дешифровки составляет 1 секунду, а для значений p = 409 и q = 419 - 2 минуты 55 секунд. При этом зависимость не является линейной.
В дальнейшем планируется исследовать влияние атаки Винера на устойчивость RSA.





