ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ДЛЯ СЧЁТНЫХ СИСТЕМ ОДУ

AN EXISTENCE THEOREM FOR A SOLUTION TO A BOUNDARY VALUE PROBLEM FOR COUNTABLE SYSTEMS OF ODES

Madina Gazdieva

Student of Ingush State University, Russia, Magas

Ismail Tankiev

Scientific adviser, Сandidate of physical and mathematical sciences, Head of the Department of Mathematical Analysis, Professor, Ingush State University, Russia, Magas

Аннотация. В данной статье рассматривается теорема существования решения линейной краевой задачи для счётных систем обыкновенных дифференциальных уравнений, а также её доказательство.

Abstract.  This article discusses the existence theorem for the solution of a linear boundary value problem for countable systems of ordinary differential equations, as well as its proof.

Ключевые слова: линейная краевая задача, интегральные уравнения, счётные системы ОДУ, существование решения.

Keywords: linear boundary value problem, integral equations, counting systems of ODE, existence of a solution.

Рассматривается счетная система обыкновенных дифференциальных уравнений

с краевыми условиями

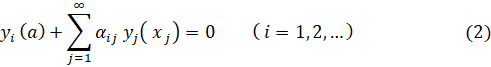
где    ( j = 1, 2, …), а  - некоторые действительные числа, такие что

Главный определитель этой системы

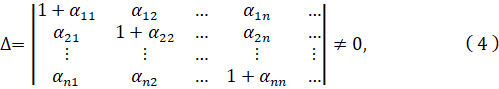
а  алгебраические дополнения s – го элемента  j - го столбца

Причем

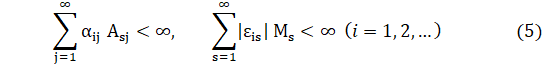
Теорема : Пусть для задачи  (1), (2) выполнены условия (3), (4), (5) и кроме того

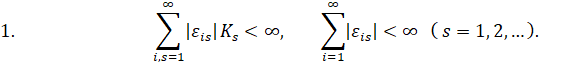
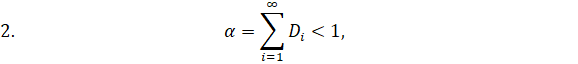
где

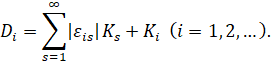
Тогда в области  G, где

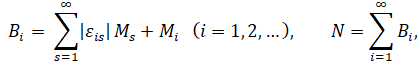
задача (1), (2) имеет по крайней мере одно непрерывное решение

Если же при этом

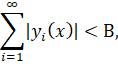
то решение будет единственным.

Доказательство: В силу эквивалентности (1), (2) и

достаточно доказать справедливость теоремы для (6).

Определим последовательность функций

на  формулами

, … ,  = 0, …

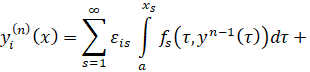
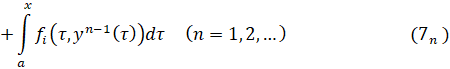
При  n = 1 имеем

Функции   непрерывны на причем

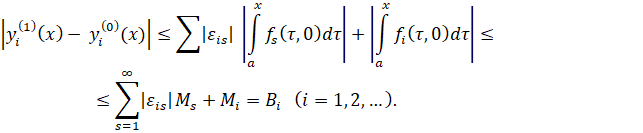
Отсюда

т.e. .

 Аналогично, расписывая  (при , из (, и вычитая его из ( оценим:

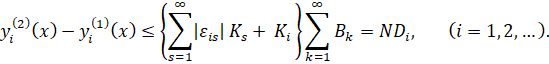
Тогда

т.е   

Применяя метод математической индукции, доказывается, что  приближение имеет смысл, т.е. непрерывно причем

Итак, получено n последовательностей непрерывных на функций не выходящих из G. Так как

то функции  являются частичными суммами рядов

которые, в силу предыдущих оценок, мажорируются числовыми рядами

сходящимися абсолютно и равномерно.

Поэтому

причем сходимость будет равномерной.   

Теперь несложно показать, что

является решением

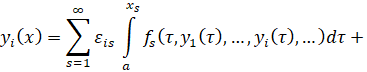
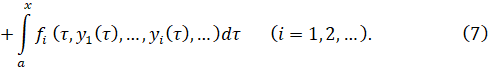
Во-первых, из метода получения очевидно,    

Введем обозначения:

Покажем, что  Согласно n-му приближению имеем:

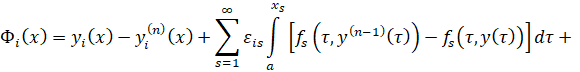
Оценивая  с учетом условия 1)   имеем но в виду произвольности  и следует

Этим показано существование решения системы (7).